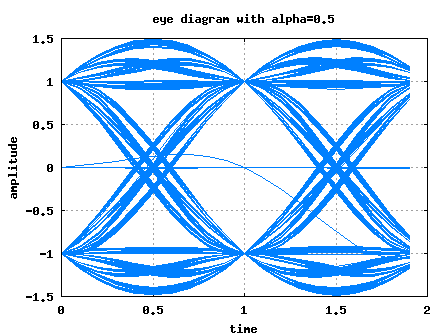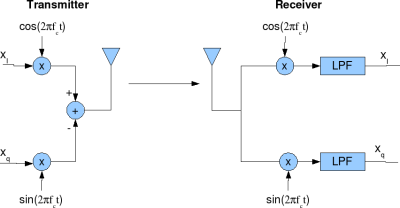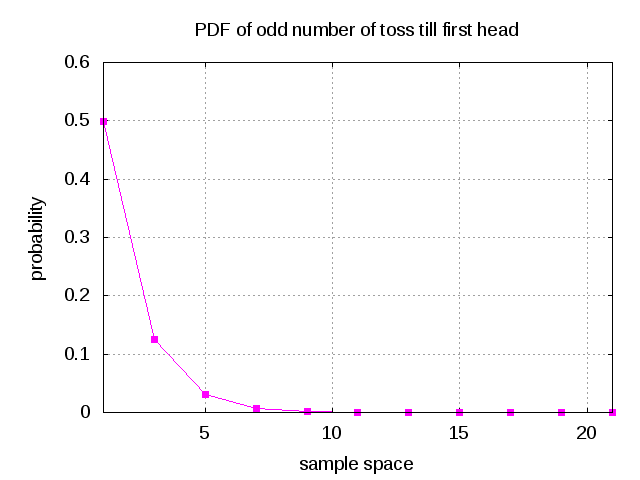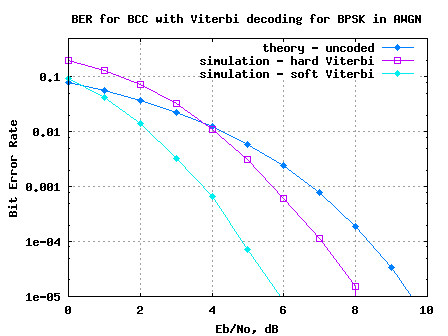
Equal Gain Combining (EGC)
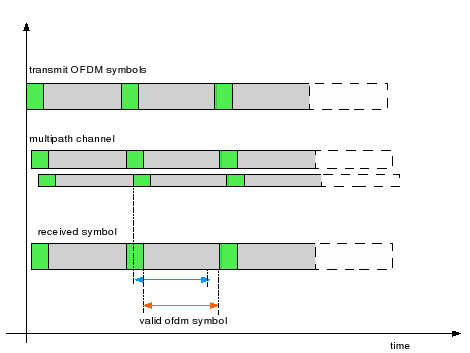
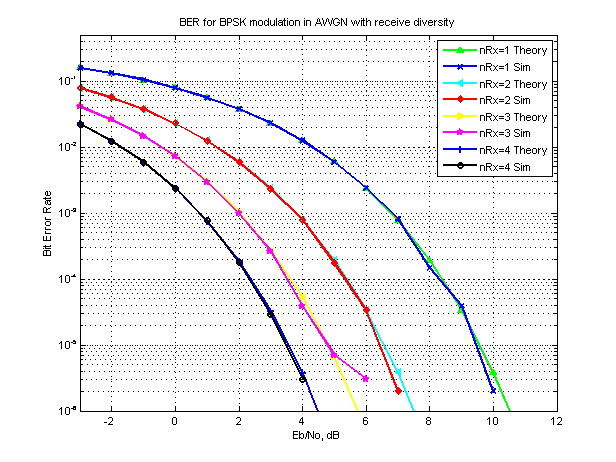
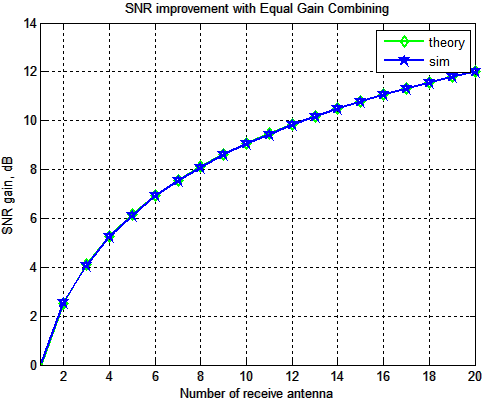
This is the second post in the series discussing receiver diversity in a wireless link. Receiver diversity is a form of space diversity, where there are multiple antennas at the receiver. The presence of receiver diversity poses an interesting problem – how do we use ‘effectively‘ the information from all the antennas to demodulate the…