In this post, let us discuss a simple implementation friendly scheme for computing the absolute value of a complex number . The technique called
(alpha Max + beta Min) algorithm is discussed in Chapter 13.2 of Understanding Digital Signal Processing, Richard Lyons
and is also available online at Digital Signal Processing Tricks – High-speed vector magnitude approximation
The magnitude of a complex number is
.
The simplified computation of the absolute value is
where
.
The values of and
can be tried out to understand the performance. For analysis we can use a complex number with magnitude 1 and phase from 0 to 180 degrees.
Option#1
= 1,
= 1/2,
Option#2
= 1,
= 1/4,
Option#3
= 1,
= 3/8
Option#4
= 7/8,
= 7/16
Option#5
= 15/16,
= 15/32
Simulation Model
The script performs the following.
(a) Generate a complex number with phase varying from 0 to 180 degrees.
(b) Find the absolute value using the above 5 options
(c) For each option, find the maximum error, average error and root mean square error
Click here to download Matlab/Octave script for computing the approximate value of magnitude of a complex number
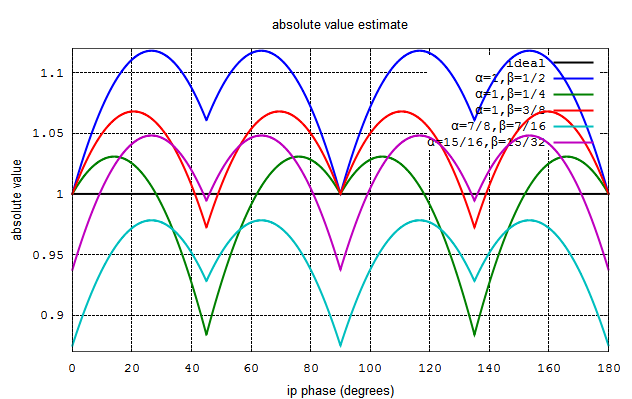
Figure: Plot of approximate value of magnitude of a complex number
| Option | alpha | beta | Maximum Error % | Average Error % | RMS error % |
| 1 | 1 | 1/2 | 11.80340 | 8.67667 | 9.21159 |
| 2 | 1 | 1/4 | -11.60134 | -0.64520 | 4.15450 |
| 3 | 1 | 3/8 | 6.80005 | 4.01573 | 4.76143 |
| 4 | 7/8 | 7/16 | -12.50000 | -4.90792 | 5.60480 |
| 5 | 15/16 | 15/32 | -6.25000 | 1.88438 | 3.45847 |
Table: Error in the approximate value computation with various values of ,
Observations
1. The chosen values of ,
facilitates simple multiplier-less implementation of approximate computation (can be implemented using only bit shift and addition).
2. For Options (1), (3) the maximum error is more than the expected value. Hence we need to allocate extra bits for the output to prevent overflow.
3. The error in the approximate magnitude computation repeats every 90 degrees.
Reference
Chapter 13.2 of Understanding Digital Signal Processing, Richard Lyons
nice,thanks a lot.
Hi krishna…
I am Firdaus from Indonesia. I have read your book “array signal processing” and i am interested about ESPRIT algorithm…But I have a problem how to change TLS esprit algoritm for Uniform linier array to Uniform Circular Array. Would you please help me to solve the problem???
best regard
Firdaus
@Firdaus: Are you sure, its me? I have never written a book on Array Signal Processing. Hopefully, I write a book some day….
Anyhow, I am not familiar with the ESPRIT algorithm.
Good, thanks!
Thanks a lot Krishna !! Could not find info related to this topic anywhere else.
Good post.
Noticed a typo – in description of Option #3, Beta has to be 3/8, and not 1/4.
@Sudeep: Thanks, I corrected the typo 🙂