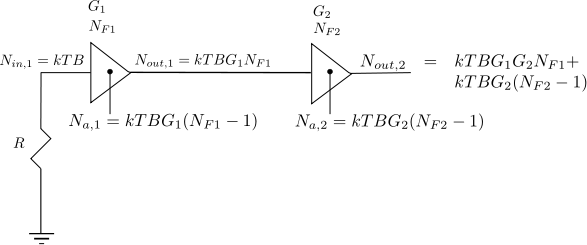
Noise Figure of cascaded stages
Following the discussion on thermal noise and it’s modeling and noise figure computation for a simple resistor network, in this article let us discuss the Noise Figure of cascaded stages.

Following the discussion on thermal noise and it’s modeling and noise figure computation for a simple resistor network, in this article let us discuss the Noise Figure of cascaded stages.
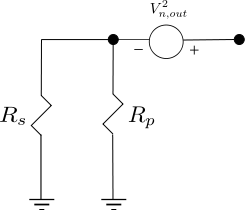
The post on thermal noise described the noise produced by resistor ohms over bandwidth at temperature Kelvin. In this post, let us define the noise voltage at the input and output of a resistor network and further use it to define the Noise Figure of such a network.
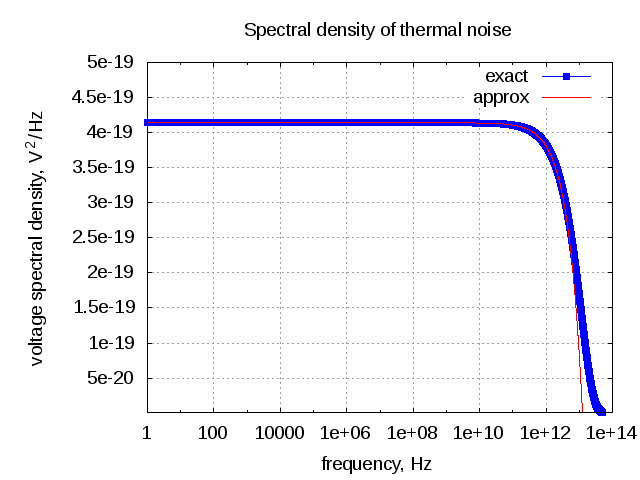
A friend called me up couple of days back with the question – How white is AWGN? I gave him an answer over phone, which he was not too happy about. That got me thinking bit more on the topic and the result is this post – brief write up on thermal noise and it’s…

An earlier post we discussed hard decision decoding for a Hamming (7,4) code and simulated the the bit error rate. In this post, let us focus on the soft decision decoding for the Hamming (7,4) code, and quantify the bounds in the performance gain.

In May 2008, we derived the theoretical symbol error rate for a general M-QAM modulation (in Embedded.com, DSPDesignLine.com and dsplog.com) under Additive White Gaussian Noise. While re-reading that post, felt that the article is nice and warrants a re-run, using OFDM as the underlying physical layer. This post discuss the derivation of symbol error rate for a general…
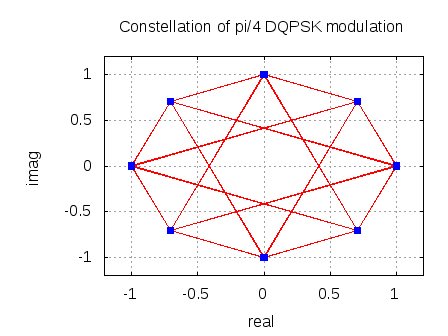
In TETRA specifications, one of the modulation technique used is Differential Quaternary Phase Shift Keying (DQPSK). We will discuss the bit error rate with non-coherent demodulation of DQPSK in Additive White Gaussian Noise (AWGN) channel.
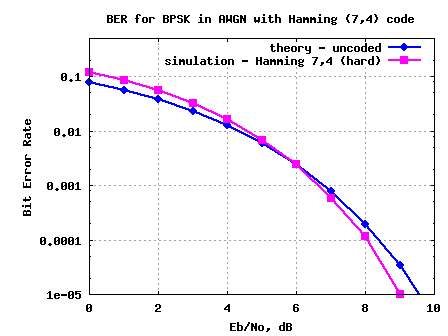
In previous posts, we have discussed convolutional codes with Viterbi decoding (hard decision, soft decision and with finite traceback). Let us know discuss a block coding scheme where a group of information bits is mapped into coded bits. Such codes are referred to as codes. We will restrict the discussion to Hamming codes, where 4…
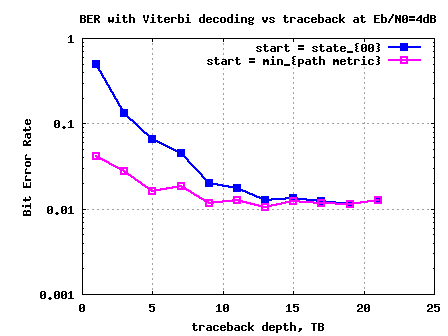
In the post on Viterbi decoder and soft input Viterbi decoder, we discussed a convolutional encoding scheme with rate 1/2, constraint length and having generator polynomial and having generator polynomial . If the number of uncoded bits is , then the number of coded bits at the output of the convolutional encoder is . Decoding…
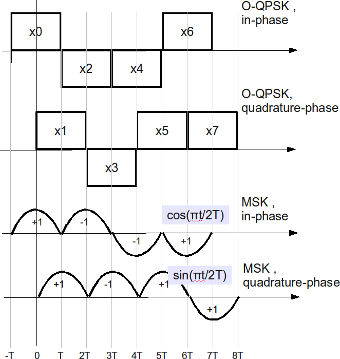
In a post on Minimum Shift Keying (MSK), we had discussed that MSK uses two frequencies which are separated by and phase discontinuity is avoided in symbol boundaries. In that post, we had discussed MSK as a continuous phase transmit signal and showed that phase changes through 0, 90, 180 and 270 degrees. In this…
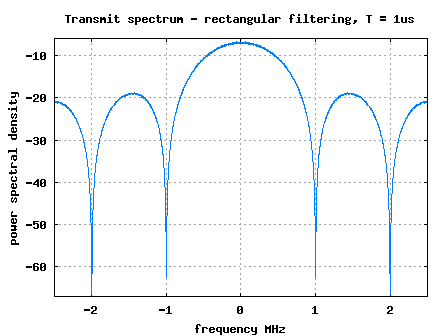
In the post on transmit pulse shaping filter, we had discussed pulse shaping using rectangular and sinc. In this post we will discuss about optimal receiver structure when pulse shaping is used at the transmitter. The receiver structure is also called as matched filter. For the discussion, we will assume rectangular pulse shaping, the channel…
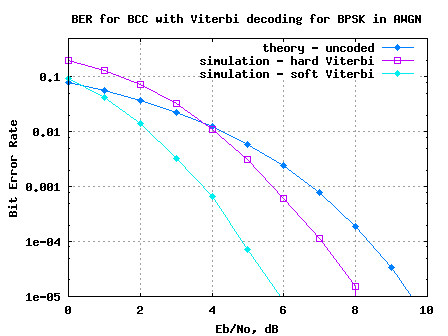
In two previous posts, we have discussed Convolutional Coding and the associated hard decision Viterbi decoding. In this post lets extent Viterbi decoding algorithm to soft input decision scheme. The modulation used is BPSK and the channel is assumed to be AWGN alone.
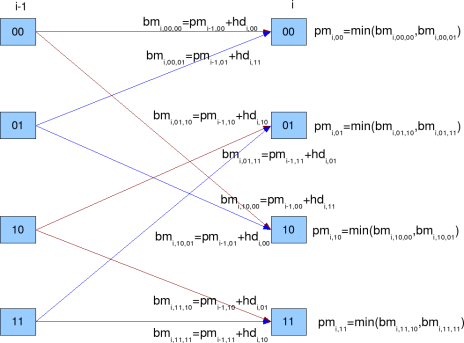
Coding is a technique where redundancy is added to original bit sequence to increase the reliability of the communication. Lets discuss a simple binary convolutional coding scheme at the transmitter and the associated Viterbi (maximum likelihood) decoding scheme at the receiver. Update: For some reason, the blog is unable to display the article which discuss…
We have quite a few articles discussing bit and symbol error rates for popular digital modulation schemes in Additive White Gaussian Noise (AWGN) channel. This post summarizes the articles discussing the theoretical and simulated error rates for the digital modulation schemes like BPSK, QPSK, 4–PAM, 16PSK and 16QAM. Further, Bit Error Rate with Gray coded…
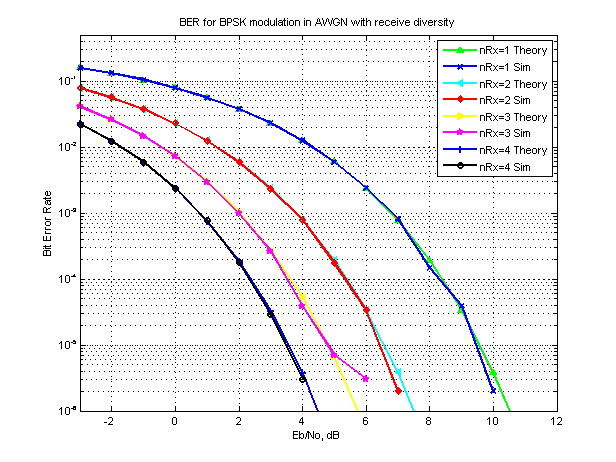
Some among you will be aware that in a wireless link having multiple antenna’s at the receiver (aka receive diversity) improves the bit error rate (BER) performance. In this post, let us try to understand the BER improvement with receive diversity. And, since we are just getting started, let us limit ourselves to additive white…