In two previous posts, we have discussed Convolutional Coding and the associated hard decision Viterbi decoding. In this post lets extent Viterbi decoding algorithm to soft input decision scheme. The modulation used is BPSK and the channel is assumed to be AWGN alone.
System Model
The received coded sequence is
, where
is the modulated coded sequence taking values
if the coded bit is 1 and
if the coded bit is 0,
is the Additive White Gaussian Noise following the probability distribution function,
with mean
and variance
.
The conditional probability distribution function (PDF) of if the coded bit is 0 is,
.
Conditional probability distribution function (PDF) of if the coded bit is 1 is,
.
Euclidean distance
In the hard decision Viterbi decoding, based on the location of the received coded symbol, the coded bit was estimated – if the received symbol is greater than zero, the received coded bit is 1; if the received symbol is less than or equal to zero, the received coded bit is 0.
In Soft decision decoding, rather than estimating the coded bit and finding the Hamming distance, the distance between the received symbol and the probable transmitted symbol is found out.
Euclidean distance if transmitted coded bit is 0 is,
.
Euclidean distance if transmitted coded bit is 1 is,
.
As the terms ,
,
and
are common in both the equations they can be ignored. The simplified Euclidean distance is,
and
.
As the Viterbi algorithm takes two received coded bits at a time for processing, we need to find the Euclidean distance from both the bits.
Summarizing, in Soft decision decoding, Euclidean distance is used instead of Hamming distance for branch metric and path metric computation.
Note:
For details on branch metric, path metric computation and trace back unit refer to the post on hard decision Viterbi decoding.
Simulation Model
Octave/Matlab source code for computing the bit error rate for BPSK modulation in AWGN using the convolutional coding and soft decision Viterbi decoding is provided.
The simulation model performs the following:
(a) Generation of random BPSK modulated symbols +1’s and -1’s
(b) Convolutionally encode them using rate -1/2, generator polynomial [7,5] octal code
(c) Passing them through Additive White Gaussian Noise channel
(d) Received soft bits and hard bits are passed to Viterbi decoder
(e) Counting the number of errors from the output of Viterbi decoder
(f) Repeating the same for multiple Eb/No value.
Click here to download Matlab/Octave script for computing BER for BPSK with AWGN in soft decision Viterbi decoding
(Warning: The simulation took around 5 hours in desktop to generate the plots)
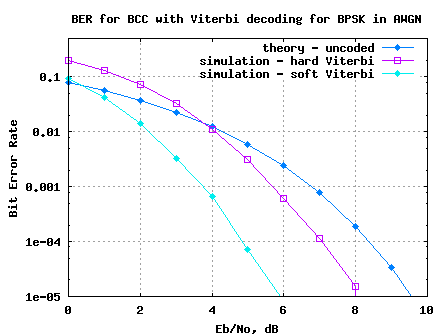
Figure: BER plot for BPSK with AWGN in soft decision Viterbi decoding
Summary
1. When compared with hard decision decoding, soft decision decoding provides around 2dB of gain for bit error rate of .
2. In the current simulation model, soft bit are used with full precision for obtaining the BER curves. However in typical implementations, soft bits will be quantized to finite number of bits.
Hi,
I don’t understand because to obtaining the noise, it use the Ec (coded signal). However, finally the figure show Eb/No and not Ec/No. Could you explain me it?
Thanks.
@insanbor: In this simulation, each 2 coded bits correspond to one raw bit (coding rate = 1/2)
So, Ec/N0,dB = Eb/N0,dB + 10*log10(coding rate);
Hi Sir,
Can you tell me if you can get a matlab code for (Convolutional BPSK over AWGN) not that one you provided in this website please.
Thanks
@Mohammed: Where you referring to convolutional code?
https://dsplog.com/2009/01/04/convolutional-code/
https://dsplog.com/tag/viterbi/
hi ;
I write the program of viterbi algorithm and run this , my algorith is true to 10^-5, but for high snr my figure cant down this number, even I increase the number of data untile 1e6
@aryana: For a no-noise case, are you getting zero BER?
Good Day Krishna,
I am studying your .m file especially the decoding part, i would like to ask if what does the matrix ipLUT came from and used for? I am very new with viterbi so pardon me with my question…
Thanks…
regards,
John
Hi Krishna, Thanks for your response. I came to know about an formula for for finding the branch metrics in soft decoder.
BM00 = y0+y1
BM01 = y0+(n-y1)
BM10 = (n-y0)+y1
BM11 = (n-y0)+(n-y1)
Where, y0 and y1 are received data pairs and n is the number of quantization levels (for 3 bit soft decoding, n=7).
Well, Can I use this formula directly to find the branch metrics for both offset-binary and signed-magnitude.
@sridar: Well, I guess you wanted to convert the floating point representations of y1, y2 to fixed point, and I do not see that happening in the equation you listed above.
I would have expected it to be something as simple as
y0_quant = round(y0*2^N)
y1_quant = round(y1*2^N)
Agree?
My intention is not to convert the floating point into fixed point representation. This is to calculate the euclidean distance, as I read. It performs the simple binary addition/subtraction to calculate the hamming distance between the received data pair y0,y1 and the binary representations of 0 and 1. say BM00 calculates the euclidean distance between encoded data pair (0,0) to the received pair(y0,y1)
@sridar: ok. for hard decision viterbi please refer to the post
https://dsplog.com/2009/01/04/viterbi/
Hi Krishna
Your blog is very good and well descriptive.
If I want to generalize my program for soft viterbi decoding for any
trellis structure, what do you think about the best approach? I do not
want to use MATLAB’s vitdec or poly2trellis function. For example,
K =7, [133,171] code is very widely used. Optimizing the code for
this is truly cumbersome. I am simulating BICM-OFDM system.
Do you suggest how should I approach to incorporate this, as in
your program you first set a look up table, which is hard for
64 state decoder.
another (may be silly) question: You used
refHard = [0 0 ; 0 1; 1 0 ; 1 1 ];
refSoft = -1*[-1 -1; -1 1 ;1 -1; 1 1 ];
……
s = 2*cip-1;
Why (-1) factor outside bracket in refSoft?
You are using 0–> -1 and 1–> 1 ..right?
A quick answer is well appreaciated. Thanks.
Toufiq
@Toufiq: You are right. 0 is -1 and 1 is 1
Hi, I want to implement soft-decision viterbi in FPGA. I would like to know how to normalize the number of bits in ACS (Add-Compare-Select) block of viterbi decoder if i use euclidean-distance instead of hamming distance.
@sridar: One simple method for normalization is to divide all the numbers in the pathmetric once all the path metric values are above a threshold. For example, if path metric is on 8bits (0 to 255), once all path-metric values are greater than 127, then divide the path metric by 2.
Could you please, help in calculating the Huffman compression ratio and the right way to make evaluation between the two signals before encoding and after decoding?
@Abdel: Sorry, I have not written any post on Huffman coding.
thanx …..
hello krishna,
can u tell me what can be the max inputsto the viterbi decoder ? i have a frame of 2048 bits. after encoding i get 4096 bits. then im doing 3-bit quantization. so total no. of bits in a frame is 12288, which is entering the decoder serially. so shud i first build the trellis upto that many number and then start the trace back?
after these bits also my input frames are coming continuously. so whether the rest frames have to wait until the decoder has decoded the first frame completely?
plz do reply…….
@mansi:
“>>then im doing 3-bit quantization. so total no. of bits in a frame is 12288, ”
This is wrong. The 3 bit quantization does not mean you have 3 bits for each coded bit. It means that each coded bit is represented by an integer which can take values from [0 7] (or [-4 to 3] depending on your representation).
ok.. thanx for that info .. but what about the other parts of my doubt…plz do reply..
@mansi: Well, ideally the Viterbi decoder needs to wait till the full frame is done prior to attempting traceback for the packet. However, simulations have shown that even if we do not wait for the whole frame to be complete prior to attempting traceback, the penalty is minimal.
Hi,
Can You please explain fact that You using in code for ii==1, all states and branch and path metric calculation and not just calculations for states 00 and 10 as explain in hard Viterbi.
Thanks
@Melinda: Well, were you refering to the code? In the code, I can see that cases ii=1,2 are treated as special cases (as done for hard decision decoding).
Hi,
On http://en.wikipedia.org/wiki/Viterbi_decoder , for soft(Euclidean) metric we can find max instead min between two branch metrics, and You use min (in code) if I’m right? Can You explain this?
Thanks
@Melinda: We need to find the difference between the ideal and the received constellation i.e.
min(r-x)^2 = min(r^2 -2rx + x^2).
Since r^2 and x^2 are contants, the equation reduces to
min(-rx) = max(+rx).
Agree?
Hi Krishna,
I agree, but why then You use min function in source code? If I’m right, You use min(+rx) not min(-rx). Or maybe this line:
refSoft = “-1” *[-1 -1; -1 1 ;1 -1; 1 1];
can explain this. Is “-1” factor reason why You use min. Could we use max instead min if we “-1” factor change to “+1″?
What is little bit strange to me, is why You use this mapping:”c is the modulated coded sequence taking values +sqrt(Ec) if the coded bit is 1 and -sqrt(Ec)if the coded bit is 0”, and in all other posts You use (-1)^b mapping. Can You also explain this?
Thanks
@Melinda: My replies
a). Yes, please try. Make it to +1 and use max. Ofcourse, the best thing we learn by trial and error.
b). Did not quite understand. What is the factor b in (-1)^b?
In most of the posts, I recall I define 0 as -1 and 1 as +1. The factor sqrt(Ec) is a scaling factor which maybe ignored.
hey could u tell me how to relate the bit error rate given in ur code to the Upper bound for bit error probabilty with SDD and HDD in viterbi. specifically, i want to plot the graph fr bounds as given in Equation 8.2-15 proakis 5th edition and get the corresponding graph as in Figure 8.2-1
Hi,
Can You explain in short, how we would calculate Euclidean distances for case 16QAM modulation and soft Viterbi?
Thanks
@Melinda: I think, soft decision for 16-QAM requires a seperate post. I hope to write soon on that topic.
i did the Soft and hard decision viterbi perfromance analysis.
I did it with a Convolutional encoder of rate 1/2 (no puncturing) and got the BER curve as mentioned by you.
Next time, i used punctured 3/4 rate with a convolution encoder of rate 1/2.
But with hard decision, i am getting a BER of 0.5 always even without any noise. At decoder input, i inserted all punctured bits as ‘0’. I got the same result if i inserted ‘1’ as punctured bits instead of ‘0’. Can you help me in this regard?
@Amit: Yes, I also just quickly tried – am getting a non zero bit error rate for infinte SNR with puncturing. Maybe we are some aspect, let me try to read more. Btw, did you try with soft decision decoding and replace the punctured bits with 0.
Please do post your findings, if you come up with the answer. Thanks.
Hi,
I have a project on error control coding. I am working on it but I am not that great at coding. If you can just help me with viterbi encoding and decoding for both soft and hard decision for rate 1/3. I saw your posts but they have rate 1/2. Everything else is same, right from BER vs EbNo plot over AGWN channel.
Thanks
@Viten: Am reasonably sure that, once you understand the concept, you should be able to adapt this code to handle the rate 1/3 case. Good luck in your coding assignments.
Hello,
I want to know that how can i use this code for rate 1/3 convolutional code with constraint length=9 and generator polynomials g0=557, g1=663 and g2=711. thanks in advance for your cooperation.
@tabenda: Hmm… no. This Viterbi code is tuned for rate 1/2, K = 3, [7,5]_8 convolutional code.
Hi,
Is it mistake or…(last line in formula for calculating Euclidean distance above):
ed11=(+yi,1 + yi,2)
is it maybe: ed11=(-yi,1 – yi,2) ?
@Melinda: Yes, you are correct. I corrected the typo. Thanks for noticing and reporting it.
Hi there,
The codes that you provided only work for coderate = 1/2 right?
if the code rate is 5/8… do you think it is advisable to use the matlab function?
@Allyson: Yes, this post is for rate 1/2. If rate 5/8 was achieved by puncturing, at the receiver you may replace the punctured bits by zeros.
I have to say, I could not agree with you in 100%, but it’s just my opinion, which could be wrong.
p.s. You have a very good template for your blog. Where did you find it?
@ automotive floor jack: Is this a spam comment?
HI,
i am implementing a 4D TCm demodulator.
i am not sure how the demapper works?
@Zeba: Sorry, I have not studied in detail Trellis Coded Modulation. Hope to do so in future.
Hi Krishna,
Just to say at beginning, that your web site rules!
Few questions for You: I developed soft demmaper(exact LLR Algorithm) and test with my own S.I.V.D. and results I get, are very close to teoretical(almost identical). But after while, I ask my self is my LLR algorithm good. Why I say that?-If You look Exact LLR Algorithm on mathworks site(just type in google: Mathworks exact LLR algorithm), you will see : L(b)=log(Pr(b=0|r=(x,y)) / Pr(b=1|r=(x,y))) , and below full formula with comments. My question actualy is: does Pr(b=0|r=(x,y)) + Pr(b=1|r=(x,y)) = 1 ? Why I ask that – if You look below full formula(on web site) if we say use BPSK modulation((-1)^bo is mapping – i.e. bit 0->1, bit1->-1) and we lets say receive channel (AWGN) symbol 0+0i, and if we calculate those probabilities we will get L(b)=log{ exp(-1/(No/2)) / exp(-1/(No/2)) }, and if You notice, upper and lower exp(…) expression are the same(someone could say they must be each = 0.5, if Pr(b=0|r=(x,y)) + Pr(b=1|r=(x,y)) = 1; is correct /or not hmm?), and lets say that No = 1 (i.e. for SNR = 0dB -> No=10^(-SNR/10)=1), and so expression: exp(-1/(No/2)) will be equal 0.1353. and we now have that those two(upper and lower) probabilities are the same but their sum is not = 1;!!! Can You please explain to me am I correct or I am wrong with my claims. Does sum of Pr(b=0|r=(x,y)) and Pr(b=1|r=(x,y)) must be equal 1 when we calculate LLRs? If that is true how You look on my simple example – am I correct(and let me remind You – I get very good results with my calculation of this LLRs (on QPSK, 16QAM…) and in my case like I explain sum of this two, upper and lower probabilites are not 1!). Can You please give some kind explanation on this.
Thank You and best regards.
@Melinda: I know, a reply is pending from me. I will look into this over the weekend and respond. Sorry for the delay.