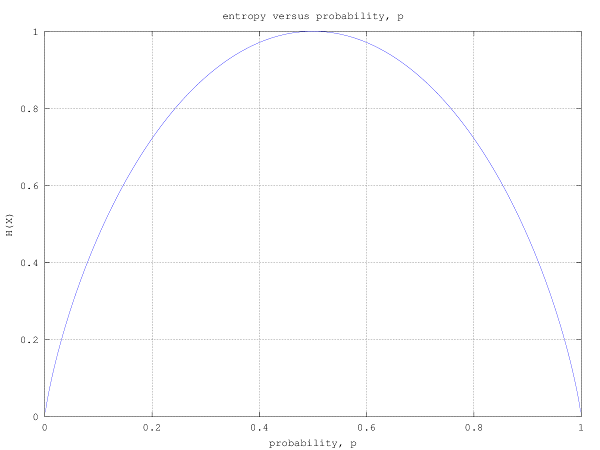
GATE-2012 ECE Q28 (electromagnetics)

Question 28 on electromagnetics from GATE (Graduate Aptitude Test in Engineering) 2012 Electronics and Communication Engineering paper.

Q28. A transmission line with a characteristic impedance of 100 ${\Omega}$ is used to match a 50 ${\Omega}$ section to a 200 ${\Omega}$ section. If the matching is to be done both at 429MHz and 1GHz, the length of the transmission line can be approximately

(A) 82.5cm

(B) 1.05m

(C) 1.58m

(D) 1.75m

Solution

To answer this question, let us first understand the propagation in a transmission line, termination and the concept of impedance matching. The section 2.1 in Microwave Engineering, David M Pozar (buy from Amazon.com, Buy from Flipkart.com) is used as reference.

Consider a transmission line of very small length $\Delta z$ having the parameters as show in figure below.

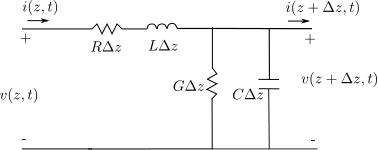
Figure : Transmission line model (Reference Figure 2.1 in Microwave Engineering, David M Pozar (buy from Amazon.com, Buy from Flipkart.com)

$R$ is the resistance per unit length $\Omega/m$ ,

$L$ is the inductance per unit length $H/m$ ,

$G$ is the conductance per unit length $S/m$ ,

$C$ is the capacitance per unit length $F/m$ .

Applying Kirchoff’s voltage law,

$v(z,t)-R\Delta zi(z,t)-L\Delta z\frac{\partial i(z,t)}{\partial t}-v(z+\Delta z ,t)=0$

Applying Kirchoff’s current law,

$i(z,t)-G\Delta zv(z+\Delta z,t)-C\Delta z\frac{\partial v(z+\Delta z,t)}{\partial t}-i(z+\Delta z ,t)=0$

Dividing the above equations by $\Delta z$ and taking the limit $\Delta z \rightarrow 0$ ,

$\frac{\partial v(z,t)}{\partial z}=-Ri(z,t) - L\frac{\partial i(z,t)}{\partial t}$

$\frac{\partial i(z,t)}{\partial z}=-Gv(z,t) - C\frac{\partial v(z,t)}{\partial t}$

If we assume that the inputs are sinusoidal, then the above equation can be re-written as

$\frac{dV(z)}{dz}=-(R+jwL)I(z)$

$\frac{dI(z)}{dz}=-(G+jwC)V(z)$

Substituting,

$\frac{d^2V(z)}{dz}-\gamma^2V(z)=0$ ,

$\frac{d^2I(z)}{dz}-\gamma^2I(z)=0$ ,

where

$\gamma=\alpha+j\beta = \sqrt{(R+jwL)(G+jwC)}$ .

The solution to the above equations are,

$V(z) = V_0^+e^{-\gamma z}+V_0^-e^{\gamma z}$

$I(z) = I_0^+e^{-\gamma z}+I_0^-e^{\gamma z}$ .

The current on the line can be alternately expressed as,

$I(z) =\frac{\gamma}{R+jwL}$V_0^+e^{-\gamma z}-V_0^-e^{\gamma z}$=\frac{1}{Z_0}$V_0^+e^{-\gamma z}-V_0^-e^{\gamma z}$$ ,

where the characteristic impedance of the line is defined as,

$Z_0=\frac{R+jwL}{\gamma}=\sqrt{\frac{R+jwL}{G+jwC}}$ .

The wavelength on the line is,

$\lambda=\frac{2\pi}{\beta}$ .

Loss less transmission line case

For a lossless transmission line, we can set $R=G=0$ .

Then the propagation constant reduces to $\begin{array}\alpha=0,&\beta = \omega\sqrt{LC}\end{array}$ , the characteristic impedance is $Z_0=\sqrt{\frac{L}{C}}$ and the voltage and current on the line can be written as,

$V(z) = V_0^+e^{-j\beta z}+V_0^-e^{j\beta z}$

$I(z) =\frac{1}{Z_0}$V_0^+e^{-j\beta z}-V_0^-e^{j\beta z}$$

Terminated lossless transmission line

Consider a transmission line terminated with load impedance $Z_L$ as shown in figure below.

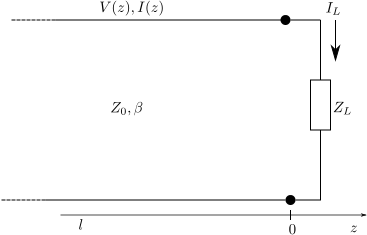
Figure: Transmission line with load impedance (Reference Figure 2.4 in Microwave Engineering, David M Pozar (buy from Amazon.com, Buy from Flipkart.com)

At the load $z=0$ , the relation between the total voltage and current is related to the load impedance $Z_L$

$Z_L=\frac{V(0)}{I(0)}=\frac{V_0^{+}+V_0^{-}}{V_0^{+}-V_0^-}Z_0$ .

Alternatively,

$V_0^{-}=\frac{Z_L-Z_0}{Z_L+Z_0}V_0^{+}$ .

The reflection coefficient $Z_L$ is defined as the amplitude of the reflected voltage to the incident voltage,

$\Gamma=\frac{V_0^{-}}{V_0^{+}}=\frac{Z_L-Z_0}{Z_L+Z_0}$ .

For no reflection to happen, i.e $\Gamma=0$ , the load impedance $Z_L$ should be equal to the characteristic impedance $Z_0$ of the transmission line. The above equation captures the impedance seen at the load $z=0$ .

The voltage and current on the line can be represented using $\Gamma$ as,

$V(z) = V_0^+$e^{-j\beta z}+\Gamma e^{j\beta z}$$

$I(z) =\frac{V_0^+}{Z_0}$e^{-j\beta z}-\Gamma e^{j\beta z}$$

When looking from a point $z=-l$ from the load, the input impedance seen is,

$\begin{array}{llllll}Z_{in}&=&\frac{V(-l)}{I(-l)}&=&\frac{V_0^{+}$e^{j\beta l} + \Gamma e^{-j\beta l}$}{\frac{V_0^{+}}{Z_0}$e^{j\beta l} - \Gamma e^{-j\beta l}$}\end{array}$ .

Substituting for $\Gamma$ ,

$\begin{array}{llllll}Z_{in}&=&Z_0\frac{$Z_L+Z_0$e^{j\beta l} +(Z_L-Z_0) e^{-j\beta l}}{$Z_L+Z_0$e^{j\beta l} -$Z_L-Z_0$ e^{-j\beta l}}\\&=&Z_0\frac{Z_L+jZ_0\tan \beta l}{Z_0+jZ_L\tan \beta l}\end{array}$ .

Special case when ${l =\lambda/4}$ (and it’s odd multiples)

For the case when ${l =$2n+1$\frac{\lambda}{4}}$ the input impedance seen is,

$\begin{array}{llll}Z_{in}&=&Z_0\frac{Z_L+jZ_0\tan \beta l}{Z_0+jZ_L\tan \beta l}\\&=&Z_0\frac{Z_L+jZ_0\tan$\frac{2\pi}{\lambda}\frac{(2n+1)\lambda}{4}$}{Z_0+jZ_L\tan$\frac{2\pi}{\lambda}\frac{(2n+1)\lambda}{4}$}\\&=&Z_0\frac{Z_0}{Z_L}=\frac{Z_0^2}{Z_L}\end{array}$ .

This result can be used to for impedance matching.

Quarter wave transformer

Consider a circuit with load $R_L$ and a line with characteristic impedance $Z_0$ connected by a transmission line of characteristic impedance $Z_1$ with length $\lambda/4$ .

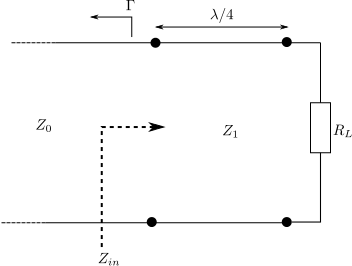
Figure: Quarter Wave Matching transformer (Reference Figure 2.16 in Microwave Engineering, David M Pozar (buy from Amazon.com, Buy from Flipkart.com)

The input impedance seen is,

$\begin{array}{llll}Z_{in}&=&Z_1\frac{R_L+jZ_1\tan \beta l}{Z_1+jR_L\tan \beta l} \\&=&Z_0\frac{Z_L+jZ_0\tan$\frac{2\pi}{\lambda}\frac{\lambda}{4}$}{Z_0+jZ_L\tan$\frac{2\pi}{\lambda}\frac{\lambda}{4}$}& \mbox{ } & $\beta l =\frac{2\pi}{\lambda}\frac{\lambda}{4}\right \pi/2$ \\&=&Z_1\frac{Z_1}{R_L}=\frac{Z_1^2}{R_L}\end{array}$ .

So if we choose $Z_1 = \sqrt{Z_0R_L}$ , then the input impedance seen is $Z_{in} = Z_0$ which is the condition required for having no reflection i.e. $\Gamma=0$ .

One important aspect to note here is that $\Gamma=0$ is not guaranteed for all frequencies, but rather only for certain frequencies. The frequency dependence can be found by finding the frequencies for which $\beta l=$2n+1$\frac{\pi}{2}$ .

Replacing $l=\frac{\lambda_0}{4}$ where $\lambda_0$ is the wave length corresponding to frequency $f_0$ ,

$\beta l = $\frac{2\pi}{\lambda}$$\frac{\lambda_0}{4}$=$\frac{2\pi f}{v_p}$$\frac{v_p}{4f_0}$=\frac{\pi f}{2 f_0}$ .

It can be seen that only for $f=$2n+1$f_0$ , the term $\beta l=$2n+1$\frac{\pi}{2}$ resulting in reflection coefficient $\Gamma=0$ only for those frequencies.

Solving the GATE question

Applying all this to the problem at hand, we have $Z_0=50$ , $R_L=200$ and $R_1=100$ .

Given that $R_1=\sqrt{Z_0 R_L} = \sqrt{50 * 200 }=100$ , we know that a quarter wave transformer is used to achieve impedance matching.

Now we also know that we need to match for two frequencies $f_{1}=429\mbox{ MHz}$ and $f_{2}=1\mbox{ GHz}$ .

The wavelength for each frequencies are,

$\lambda_{1}=\frac{3e^8}{429e^6}*100\simeq 70\mbox{ cm}$

$\lambda_{2}=\frac{3e^8}{1e^9}*100\simeq 30\mbox{ cm}$

The least common multiple of these two wavelength is, $\lambda_{lcm}=\mbox{lcm}$70,30$=210\mbox{ cm}$ and the corresponding quarter wave length is $\frac{\lambda_{lcm}}{4}=52.5\mbox{ cm}$ .

Given than $\frac{\lambda_{lcm}}{4}=52.5\mbox{ cm}$ is not listed in the options, we can go for the next higher odd multiple i.e. $52.5*3=157.5 \simeq 1.58\mbox{ m}$

Based on the above, the right choice is (C) 1.58m

References

[1] GATE Examination Question Papers [Previous Years] from Indian Institute of Technology, Madras http://gate.iitm.ac.in/gateqps/2012/ec.pdf

[2] Microwave Engineering, David M Pozar (buy from Amazon.com, Buy from Flipkart.com)

Migrated to Amazon EC2 instance (from shared hosting)