A friend called me up couple of days back with the question – How white is AWGN? I gave him an answer over phone, which he was not too happy about. That got me thinking bit more on the topic and the result is this post – brief write up on thermal noise and it’s modelling as Additive White Gaussian Noise aka AWGN.
Thermal Noise
Quoting from Chapter 9.3 of Communication Systems – An introduction to Signals and noise in Electrical Communication by A. Bruce Carlson, Paul Crilly, Janet Rutledge
“Thermal Noise is the noise produced by the random motion of charged particles (usually electrons) in conducting media.”
With a resistor ohms at temperature
Kelvins, the noise voltage
due to random electron process is a Gaussian distributed (thanks to Central Limit Theorem) variable with zero mean, and variance of
, where
is the Boltzmann constant
Joules/Kelvin,
is the Planck constant
Joules second.
The spectral density of the thermal noise is shown as,
.
Assuming and using the Taylor series approximation, the equation simplifies to :
.
Note :
a) Mr. Clay S Turner in his write up “Johnson-Nyquist Noise”, Turner C. S., Jan 2007 has derived the above expression – I did not understand the derivation – one of my many TO-DO’s. 🙂
b) The fundamental paper’s discussing this topic is (thanks to wiki entry on Johnson-Nyquist noise)
“Thermal Agitation of Electric Charge in Conductors”, (1928) H. Nyquist,
“Thermal Agitation of Electricity in Conductors”, (1928) J. Johnson,
Have not gone through both.
c) The Taylor Series results used for the approximation
From the plot of the spectral density of thermal noise over frequency, can see that the noise is flat frequency spectrum till around 100GHz or so and starts to fall off at around 1TeraHz.
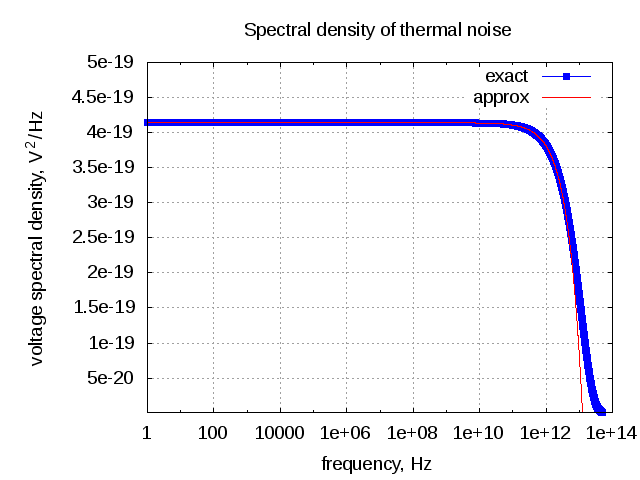
Figure : Spectral density of thermal noise
Given the above plot, for most of the practical systems which we are dealing with today (i.e. with carrier frequency less than 10GHz or so), can assume that the noise spectral density is flat, i.e.
.
Thus for a bandwidth , the root mean square noise voltage is,
The mean square voltage is,
Note :
The factor is because the noise is real with a symmetric frequency spectrum. Multiplication by 2 suffice to consider both the positive and negative frequencies.
Matlab/Octave script to get the above plot
clear all; close all;
k = 1.38e-23; % Boltzmann constant
h = 6.62e-34; % Planck's constant
T_kelvin = 300; % temperature in Kelvin
f_hz = logspace(0,14,10000);
R_ohm = 50;
Gf = 2*R_ohm*h*f_hz./(exp((h*f_hz)/(k*T_kelvin)) - 1);
Gf_approx1 = 2*R_ohm*k*T_kelvin*(1-h*f_hz/(2*k*T_kelvin));
semilogx(f_hz,Gf,'bs-');
hold on; grid on;
semilogx(f_hz,Gf_approx1,'r-');
axis([1 10^14 10^-21 0.5*10^-18]);
legend('exact', 'approx');
xlabel('frequency, Hz');
ylabel('voltage spectral density, V^2/Hz');
title('Spectral density of thermal noise');
Plugging in some numbers :
For ohms,
Temperature (26.85 deg Celsius),
Bandwidth ,
will result in rms noise voltage of
1 nano Volts
(Thanks to wiki entry on Johnson Nyquist Noise for this)
Thevenin Equivalent Model
Thevenin equivalent model of the thermal resistance noise is shown below, where the it is modeled as a voltage source in series with a noiseless resistor.
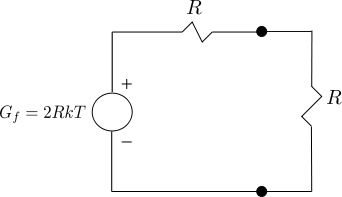
Figure : Thevenin equivalent model with matched load (Figure 9.3-3 in Communication Systems – An introduction to Signals and noise in Electrical Communication by A. Bruce Carlson, Paul Crilly, Janet Rutledge)
Assuming that the load resistance is (per maximum power transfer theorem), the rms voltage seen across the load resistance is,
The power is,
.
Note :
a) The noise power is independent of the resistance .
b) Above is the single sided noise power
Noise Power in dBm
Typically the noise power is expressed in dBm (0dBm = 1 milli Watts). The noise power in dBm for 1Hz at room temperature
In general, for a bandwidth , the noise power is
.
| Bandwidth, B Hz | Thermal noise power, dBm | Remark |
| 1 | -173.83 | for 1Hz bandwidth |
| 1,000,000 | -113.83 | For Bluetooth channel |
| 20,000,000 | -100.82 | for WLAN 20MHz channel |
| 40,000,000 | -97.81 | for WLAN 40MHz channel |
| 80,000,000 | -94.80 | for WLAN 80MHz channel |
Modeling white noise
Typically, we can write spectral density of white noise as
.
Further, from Weiner – Khinchin theorem, it is known that power spectral density and autocorrelation are Fourier transform pairs, i.e. the autocorrelation is,
.
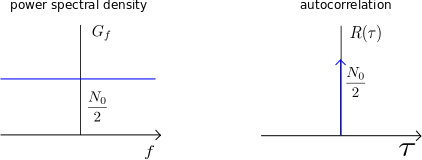
Figure : Power spectral density and autocorrelation of white noise
Note: The term 1/2 is to indicate that power is symmetric across both positive and negative frequencies.
In the simulation models used in the blog, the randn() function provided by Mathworks is used to generate White Gaussian Noise. Using a small Matlab code snippet, can see that over many realizations the simulated power spectral density tends to be white (i.e. constant across frequency).
clear all;
n_fft = 2048; n_vec = 1000;
nt = randn(n_vec,n_fft);
ntf = 1/sqrt(n_fft)*fft(nt,[],2);
ntf_pwr = ntf.*conj(ntf);
ntf_pwr_avg = mean(ntf_pwr);
plot([-n_fft/2:n_fft/2-1]/n_fft,10*log10(fftshift(ntf_pwr_avg)));
axis([-0.5 0.5 -5 5]); grid on;
ylabel('power spectral density, dB/Hz');
xlabel('normalized frequency');
title('power spectral density of white noise');
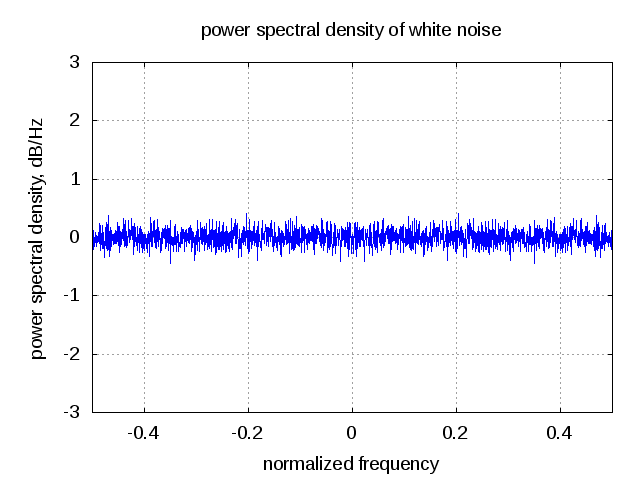
Figure : Simulated spectrum of white noise
Further, can see an impulse for the simulated auto-correlation of the noise vector generated from randn().
clear all;
n_len = 10^4;
nt = randn(1,n_len);
n_ac = 1/n_len*conv(fliplr(nt),nt);
plot([-n_len+1:n_len-1],n_ac);
xlabel('delay, tau');
ylabel('autocorrelation');
title('autocorrelation of white noise');
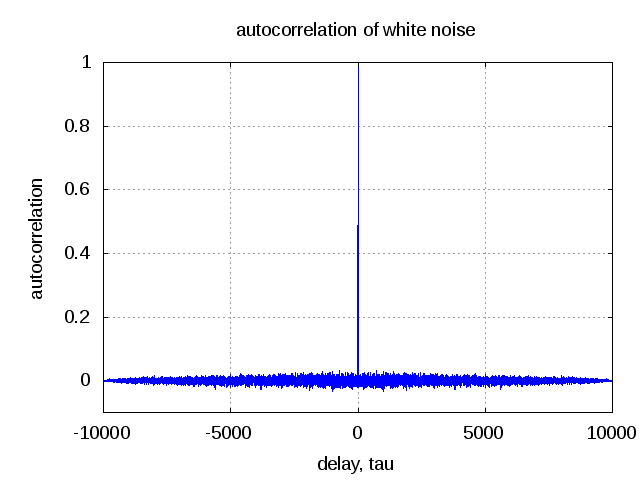
Figure : Simulated autocorrelation of white noise
References
Johnson-Nyquist Noise”, Turner C. S., Jan 2007
Wiki entry on Weiner – Khinchin theorem


WOW just what I was looking for. Came here by searching for pcb software
very useful
Thank you for your insightful discussion!!!
Nice site byt the way and now I know how the thermal noise popped up in our 44Mhz DAC discussion :-)….
@Shabeer: Thanks, lol ! 🙂
I used to believe that thermal noise and AWGN are different things until I saw this acticle. Thx for your work.
Very useful!!