This post discuss about the thermal noise in RC low pass filter. Using the noise equivalent model using resistor with a voltage source, which gets passed through a no noise RC low pass filter. The noise power at the output is computed by integrating the output voltage spectral density over all frequencies.
Consider a simple RC low pass filter with resistor and capacitance
as shown in the figure below.
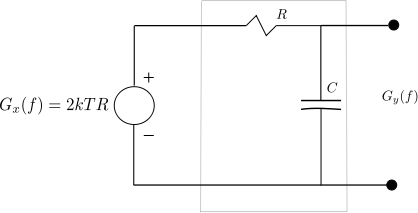
Figure : Noise equivalent model of RC low pass filter (Reference : Figure 9.3-6 in Communication Systems – An introduction to Signals and noise in Electrical Communication by A. Bruce Carlson, Paul Crilly, Janet Rutledge)
As discussed in the post on thermal noise and AWGN, the resistor is generating a noise having power
having power spectral density
.
The noise voltage gets applied to a noise less RC low pass filter having transfer function,
, where
is the -3dB bandwidth of the filter.
The power spectral density of the output signal is,
.
Integrating the output power spectral density over all frequencies from will give the noise voltage at the output, i.e.
.
Computing by plugging in the expression for
,
.
(Note: The neat trick behind integration described below)
Plugging in and
, the noise power at the output is,
.
Summarizing, the mean square voltage at the output of the RC low pass filter is,
.
Plugging in capacitance values from 1pF to 1nF, the root mean square voltage is shown below.
| k (Boltzmann constant) | 1.38E-023 | Joules/Kelvin |
| T (temperature) | 300 | Kelvin |
| Capacitance, farad | RMS voltage, V | |
| 1.00E-012 | 6.434E-005 | |
| 1.00E-011 | 2.035E-005 | |
| 1.00E-010 | 6.434E-006 | |
| 1.00E-009 | 2.035E-006 |
Observations:
a) As expected from the equation, when the capacitance is increased, the noise voltage reduces (as the filter bandwidth is getting narrower).
b) The noise power at the output is independent of resistor . Increasing the resistance will increase the noise power
, but decreases the filter bandwidth
. Similarly decreasing the resistor will reduce the noise power, but increases the filter bandwidth. These two effects cancel each other leaving the noise power dependent only on the temperature
and capacitance
.
References:
b) List of Trigonometric Identities from wikipedia
c) Differentiation rules from wikipedia
d) Johnson-Nyquist Noise from wikipedia
Note :
Liked the neat trick using substitution for solving the integration over all frequencies in a first order RC low pass filter. Did some googling to find that out…and the steps are as follows.
Let , then
and the integration limits are
,
.
Also, note that (thanks to the List of Trigonometric Identities from wikipedia, Differentiation rules from wikipedia)
,
Plugging all the above,
. Neat!


Thanks!! In addition, would you mind create a topic or post relate document to discuss what is interlever and puncture for channel coding?? Because your explain was very easy to know, i expect that badly, thank you!!