AWGN Archives - Page 2 of 3

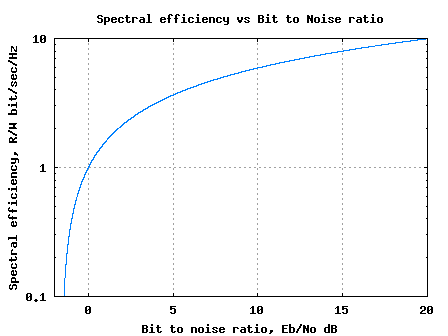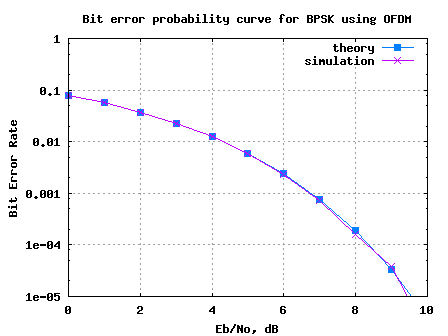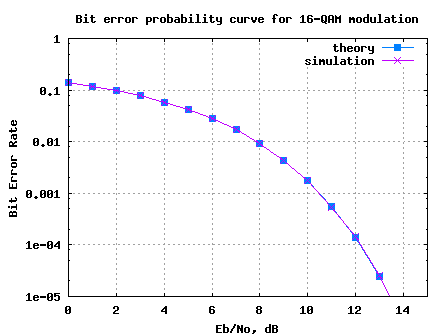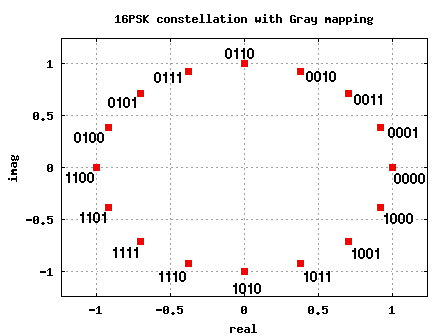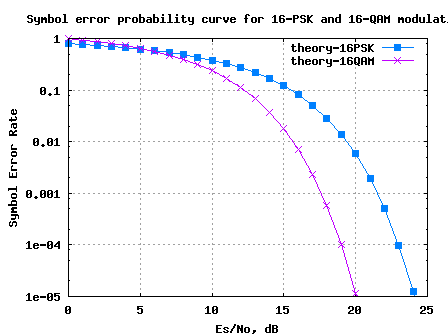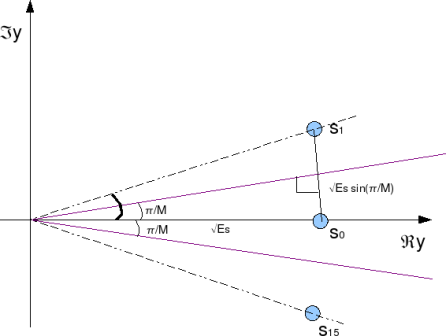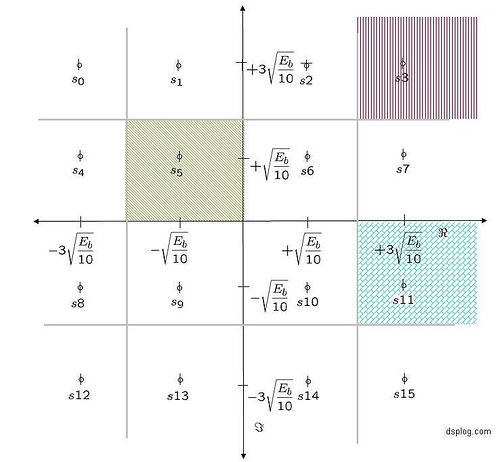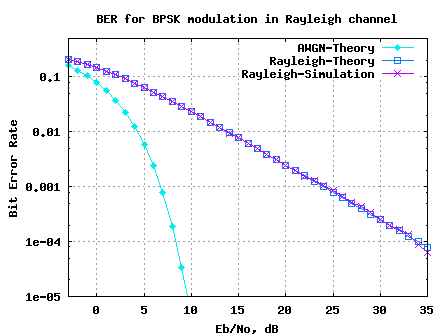
BER for BPSK in Rayleigh channel

Long back in time we discussed the BER (bit error rate) for BPSK modulation in a simple AWGN channel (time stamps states August 2007). Almost an year back! It high time we discuss the BER for BPSK in a Rayleigh multipath channel.

In a brief discussion on Rayleigh channel, wherein we stated that a circularly symmetric complex Gaussian random variable is of the form,

$h = h_{re} + jh_{im}$ ,

where real and imaginary parts are zero mean independent and identically distributed (iid) Gaussian random variables with mean 0 and variance $\sigma^2$ .

Continue reading “BER for BPSK in Rayleigh channel”

Comparing BPSK, QPSK, 4PAM, 16QAM, 16PSK, 64QAM and 32PSK

I have written another article in DSPDesginLine.com. This article can be treated as the third post in the series aimed at understanding Shannon’s capacity equation.

For the first two posts in the series are:

1. Understanding Shannon’s capacity equation

2. Bounds on Communication based on Shannon’s capacity

The article summarizes the symbol error rate derivations in AWGN for modulation schemes like BPSK, QPSK, 4PAM, 16QAM, 16PSK, 64QAM and 32PSK.

Continue reading “Comparing BPSK, QPSK, 4PAM, 16QAM, 16PSK, 64QAM and 32PSK”

Bounds on Communication based on Shannon’s capacity

This is the second post in the series aimed at developing a better understanding of Shannon’s capacity equation. In this post let us discuss the bounds on communication given the signal power and bandwidth constraint. Further, the following writeup is based on Section 12.6 from Fundamentals of Communication Systems by John G. Proakis, Masoud Salehi

Continue reading “Bounds on Communication based on Shannon’s capacity”

Understanding Shannon’s capacity equation

Let us try to understand the formula for Channel Capacity with an Average Power Limitation, described in Section 25 of the landmark paper A Mathematical Theory for Communication, by Mr. Claude Shannon.

Further, the following writeup is based on Section 12.5.1 from Fundamentals of Communication Systems by John G. Proakis, Masoud Salehi

Continue reading “Understanding Shannon’s capacity equation”

BPSK BER with OFDM modulation

Oflate, I am getting frequent requests for bit error rate simulations using OFDM (Orthogonal Frequency Division Multiplexing) modulation. In this post, we will discuss a simple OFDM transmitter and receiver, find the relation between Eb/No (Bit to Noise ratio) and Es/No (Signal to Noise ratio) and compute the bit error rate with BPSK.

Continue reading “BPSK BER with OFDM modulation”

16QAM Bit Error Rate (BER) with Gray mapping

Let us derive the theoretical 16QAM bit error rate (BER) with Gray coded constellation mapping in additive white Gaussian noise conditions. Further, the Matlab/Octave simulation script can be used to confirm that the simulation is in good agreement with theory.

Continue reading “16QAM Bit Error Rate (BER) with Gray mapping”

Article in DSPDesignLine.com: M-QAM symbol error

Its been a nice week for me, wherein I guest posted an article in DSPDesignLine.com. 🙂

The article derives the theoretical symbol error rate for M-QAM modulation. The theoretical results are further supplemented by Matlab/Octave simulation scripts.

Those who are familiar with derivation of symbol error rate for 16-QAM modulation will find the equations easy to interpret. As we did for 16-QAM,

Continue reading “Article in DSPDesignLine.com: M-QAM symbol error”

Bit error rate for 16PSK modulation using Gray mapping

In this post, let us derive the theoretical bit error probability for 16PSK modulation using Gray coded mapping. For deriving the equation, we will refer material from the following posts:

(a) Symbol Error Rate for 16PSK

(b) Gray code to Binary code conversion for PSK

As discussed in the previous posts, the key feature of Gray code is that adjacent symbols differ by only one bit. The 16PSK constellation with Gray mapping can be as shown in the figure below.

Continue reading “Bit error rate for 16PSK modulation using Gray mapping”

Comparing 16PSK vs 16QAM for symbol error rate

In two previous posts, we have derived theoretical symbol error rate for 16-QAM and 16-PSK modulation schemes. The links are:

(a) Symbol error rate for 16-PSK

(b) Symbol error rate for 16-QAM

Given that we are transmitting the same number of constellation points in both 16-PSK and 16-QAM, let us try to understand the better modulation scheme among the two, i.e. to answer the following question:

For the same signal to noise ratio $\frac{E_s}{N_0}$ , will 16-PSK or 16-QAM give a lower symbol error rate?

Continue reading “Comparing 16PSK vs 16QAM for symbol error rate”

Symbol Error Rate for 16PSK

In this post, let us try to derive the symbol error rate for 16-PSK (16-Phase Shift Keying) modulation.

Consider a general M-PSK modulation, where the alphabets,

$alpha_{16PSK} =\sqrt{E_s}\left\{1,\ e^{\frac{j2\pi}{M}},\ e^{\frac{j4\pi}{M}},\ \ldots,\ e^{\frac{j2\pi(M-1)}{M}} \right}$ are used.

(Refer example 5-38 in [DIG-COMM-BARRY-LEE-MESSERSCHMITT])

Figure: 16-PSK constellation plot

Continue reading “Symbol Error Rate for 16PSK”

Symbol Error Rate (SER) for 16-QAM

Given that we have went over the symbol error probability for 4-PAM and symbol error rate for 4-QAM , let us extend the understanding to find the symbol error probability for 16-QAM (16 Quadrature Amplitude Modulation). Consider a typical 16-QAM modulation scheme where the alphabets (Refer example 5-37 in [DIG-COMM-BARRY-LEE-MESSERSCHMITT]).

$\alpha_{16QAM}=\left{\pm 1+\pm 1j,\ \pm 1+\pm 3j,\\\pm 3 + \pm 3j,\ \pm 3+\pm 1j \right}$ are used.

Continue reading “Symbol Error Rate (SER) for 16-QAM”

Symbol Error Rate (SER) for QPSK (4-QAM) modulation

Given that we have discussed symbol error rate probability for a 4-PAM modulation, let us know focus on finding the symbol error probability for a QPSK (4-QAM) modulation scheme.

Background

Consider that the alphabets used for a QPSK (4-QAM) is $\alpha_{QPSK}=\left{\pm 1\ \pm 1j\right}$ (Refer example 5-35 in [DIG-COMM-BARRY-LEE-MESSERSCHMITT]).

Download free e-Book discussing theoretical and simulated error rates for the digital modulation schemes like BPSK, QPSK, 4–PAM, 16PSK and 16QAM. Further, Bit Error Rate with Gray coded mapping, bit error rate for BPSK over OFDM are also discussed.
Interested in MIMO (Multiple Input Multiple Output) communications? Click here to see the post describing six equalizers with 2×2 V-BLAST.
Read about using multiple antennas at the transmitter and receiver to improve the diversity of a communication link. Articles include Selection diversity, Equal Gain Combining, Maximal Ratio Combining, Alamouti STBC, Transmit Beaforming.

Continue reading “Symbol Error Rate (SER) for QPSK (4-QAM) modulation”

Symbol Error Rate (SER) for 4-PAM

Following discussion of bit error rate (BER) for BPSK and bit error rate for FSK, it may be interesting to move on to discuss a higher order constellation such as Pulse Amplitude Modulation (PAM).

Consider that the alphabets used for a 4-PAM is $\alpha_{4PAM}=\left{\pm 1,\ \pm 3\right}$ (Refer example 5-34 in [DIG-COMM-BARRY-LEE-MESSERSCHMITT]).

Continue reading “Symbol Error Rate (SER) for 4-PAM”

Coherent demodulation of DBPSK

In a previous post, we discussed about a probable first order digital PLL for tracking constant phase offset. The assumption was that as the phase offset is small and the bits gets decoded correctly, the phase difference between the ideal and actual constellation gives the initial value of phase. However, in typical scenarios it may be possible that the above assumption may not be valid, resulting in phase ambiguity.

Continue reading “Coherent demodulation of DBPSK”