(2 votes, average: 4.5 out of 5)

Loading ...

Symbol Error Rate (SER) for 4-PAM

by Krishna Sankar on October 7, 2007

Following discussion of bit error rate (BER) for BPSK and bit error rate for FSK, it may be interesting to move on to discuss a higher order constellation such as Pulse Amplitude Modulation (PAM).

Consider that the alphabets used for a 4-PAM is $\alpha_{4PAM}=\left{\pm 1,\ \pm 3\right}$ (Refer example 5-34 in [DIG-COMM-BARRY-LEE-MESSERSCHMITT]).

The average energy of the constellation assuming all the alphabets are equally likely is,

$\begin{eqnarray}E_{16PAM} & = & E\left[|\alpha_{4PAM}|^2\right] \\&=&\frac{1\ast2}{4}\sum\left[1^2+3^2\right]\\&=&5\end{eqnarray}$ .

The constellation plot for a 4-PAM signal after normalization can be as shown below.

Figure: Constellation plot for 4 PAM modulation

Channel Model

Now comes the interesting task – analysis of symbol error probability for the modulation scheme in additive white Gaussian noise condition. The noise $n$ follows the Gaussian probability distribution function, $p(x) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{\frac{-(x-\mu)^2}{2\sigma^2}$ with $\mu=0$ and $\sigma^2 = \frac{N_0}{2}$ .

Computing the symbol error rate

Using the derivation provided in Section 5.2.1 of [COMM-PROAKIS] as reference:

The received signal can be

$y=s_0 + n$ or $y=s_1 + n$ or $y=s_2 + n$ or $y=s_3 + n$ .

Let us first consider the case $s_3$ was transmitted.

The conditional probability distribution function (PDF) of $y$ given $s_3$ was transmitted is :

$p(y|s_3) = \frac{1}{\sqrt{\pi N_0}}e^{\frac{-\left(y-3\sqrt{\frac{E_s}{5}}\right)^2}{N_0}$ .

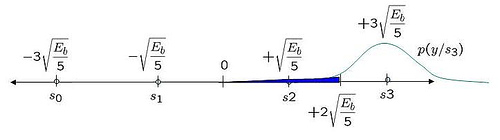
Figure: Probability distribution function when the alphabet +3 is sent

Using midway point between +1 and +3 as the detection threshold, i.e. for received signal $y>+2\sqrt{\frac{E_s}{5}} \Rightarrow s_3$ .

With this threshold, the probability of error given $s_3$ is transmitted is (the area in blue region):

$p(e|s_3) = \frac{1}{\sqrt{\pi N_0}}\int_{-\infty}^{+2\sqrt{\frac{E_s}{5}}}e^{\frac{-\left(y-3\sqrt{\frac{E_s}{5}}\right)^2}{N_0}}dy=\frac{1}{\sqrt{\pi}}\int_{\sqrt{\frac{E_s}{5N_0}}}^\infty e^{-z^2}dz=\frac{1}{2}erfc\left({\sqrt{\frac{E_s}{5N_0}}}\right)$ .

Note: The complementary error function, $erfc(x) = \frac{2}{\sqrt{\pi}}\int_x^\infty e^{-x^2}dx$ .

Given that the constellation of +3 and -3 is symmetric, it is reasonably intuitive that the probability of error given $s_0$ is transmitted is also,

$p(e|s_0) = \frac{1}{2}erfc\left({\sqrt{\frac{E_s}{5N_0}}}\right)$ .

Case where $s_2$ is transmitted

The conditional probability distribution function (PDF) of $y$ given $s_2$ was transmitted is :

$p(y|s_2) = \frac{1}{\sqrt{\pi N_0}}e^{\frac{-\left(y-\sqrt{\frac{E_s}{5}}\right)^2}{N_0}$ .

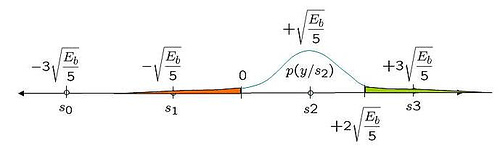
Figure: Probability distribution function when the alphabet +1 is sent

The probability of error given $s_2$ is transmitted is (the area in green and red region):

$p(e|s_2) = \frac{1}{\sqrt{\pi N_0}}\int_{-\infty}^{0}e^{\frac{-\left(y-\sqrt{\frac{E_s}{5}}\right)^2}{N_0}}dy + \frac{1}{\sqrt{\pi N_0}}\int_{+2\sqrt{\frac{E_s}{5}}}^{\infty}e^{\frac{-\left(y-\sqrt{\frac{E_s}{5}}\right)^2}{N_0}}dy=erfc\left({\sqrt{\frac{E_s}{5N_0}}}\right)$

Given that the constellation for +1 and -1 is symmetric, it is reasonably intuitive that the probability of error given $s_1$ is transmitted is also,

$p(e|s_1) = erfc\left({\sqrt{\frac{E_s}{5N_0}}}\right)$ .

Total probability of symbol error

Given that all the alphabets are equally likely, the total probability of symbol error is,

$P_s=p(s_0)p(e|s_0)+p(s_1)p(e|s_1)+p(s_2)p(e|s_2)+p(s_3)p(e|s_3)$ .

Assuming, $s_0$ and $s_1$ $s_2$ , $s_3$ are equally probable i.e. $p(s_0) = p(s_1)=p(s_2)=p(s_3)=1/4$ , the symbol error probability is,

$P_s=\frac{1}{4}\left[\frac{2}{2}erfc\left({\sqrt{\frac{E_s}{5N_0}}}\right)+2erfc\left({\sqrt{\frac{E_s}{5N_0}}}\right)\right]=\frac{3}{4}erfc\left({\sqrt{\frac{E_s}{5N_0}}}\right)$ .

Simulation Model

The Matlab/Octave script for generating a 4-PAM transmission, pass it through additive white Gaussian noise and demoduation at the receiver will be useful for understanding the concept further. The symbol error rate plots obtained from simulations compare well with the theoretical derivations.

Click here to download: Matlab/Octave script for simulating 4PAM symbol error rate

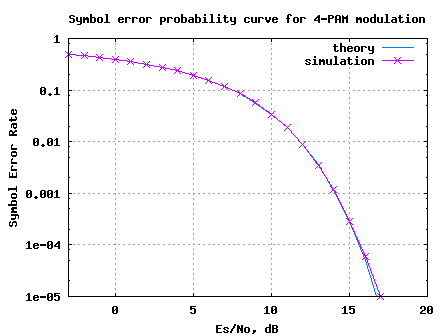
Figure: Symbol Error Rate for 4-PAM modulation

Reference

[DIG-COMM-BARRY-LEE-MESSERSCHMITT] Digital Communication: Third Edition, by John R. Barry, Edward A. Lee, David G. Messerschmitt

Tagged as: AWGN, PAM

D id you like this article? Make sure that you do not miss a new article by subscribing to RSS feed OR subscribing to e-mail newsletter. Note: Subscribing via e-mail entitles you to download the free e-Book on BER of BPSK/QPSK/16QAM/16PSK in AWGN.

{ 1 trackback }

Download free e-book on error probability in AWGN: October 1, 2008 at 9:43 pm

{ 28 comments… read them below or add one }

1 Jhony May 9, 2008 at 5:26 pm

kindly tell me from where should i start programming the communication things in MATLAB i am facing alot of difficulties. Waiting desperately for your reply …
thnks in advance

2 Krishna Pillai May 9, 2008 at 8:17 pm

@johny: Dont worry and of-course do not be desperate. Start reading the articles slowly with a clam-clear mind. Things will fall in place. In the meanwhile, I happened to see a nice article from Mathworks
“Modeling a Communications System Using the Communications Toolbox” URI: http://www.mathworks.com/products/demos/commtlbx/commsys/commsdemo.html
It goes step-by-step over the blocks in a typical communication link. Nice read.

3 Jhony May 13, 2008 at 2:26 pm

thankyou very much … the link you gave is helping me alot … you are great thanks alot once again

4 dung September 18, 2008 at 8:41 am

good

5 mohit jain November 3, 2008 at 3:31 am

You have generated the symbol error probability.
What would be the difference if i wanted to do it for bit error probability?

Thanks

6 Krishna Pillai November 5, 2008 at 6:12 am

@mohit: For BER, one would want to assign bits to constellation points (typically using Gray mapping). Then based on the received constellation point, map this to bits and count the errors.

Typically, if one assumes Gray mapping,
Pb = Ps/k.
Since each constellation carries k bits, then
Es/No = k*Eb/No.

You may refer to the posts @
http://www.dsplog.com/tag/gray/
for reference.

Hope this helps.

7 Sravani November 13, 2008 at 5:26 am

So for 4- PAM
Es/N0=2*Eb/N0
that is the only change we need to do??

8 Krishna Pillai November 15, 2008 at 8:13 am

@Sravani: Yes, since each symbol carries two bits in 4-PAM,
Es/No = 2Eb/No

9 surbhi November 24, 2008 at 3:42 pm

hello sir,
good to see such a organised blog. its all your hard work.
sir, i m working on diversity along with MSK modulation. whenever we use matlab in built function for decoding it gives an error. please tell me how to find BER using MSK modulation

10 Krishna Pillai November 25, 2008 at 5:59 am

@surbhi: I have not written a post on MSK demodulation, but have written on
(a) BER computation with FSK
http://www.dsplog.com/2007/08/30/bit-error-rate-for-frequency-shift-keying-with-coherent-demodulation/
(b) Generation of an MSK transmission
http://www.dsplog.com/2008/01/19/simulating-minimum-shift-keying-transmitter/

Hope these two posts help to achieve your goal of doing MSK with diversity. All the best.

11 somanth March 1, 2009 at 12:13 pm

i am looking for best modulation technique suitable for software radio and which parameters affect it the most.please guide me..

12 Krishna Pillai March 5, 2009 at 4:32 am: @somnath: As I see, every modulation technique has its own pros and cons. For eg.
BPSK is simpler and requiers low SNR to work, but the data rate is less.
64QAM is relatively complex, but requires high SNR to work and we have good data rate.

So, in typical systems (like 802.11a wireless LANs), one finds different data rate specifications like 6, 9, 12, … 48, 54Mps. Based on the SNR constraints, the modem adapts to an optimal data rate maximizing the throughput.

These constraints should be similiar in software defined radio too.

Hope this helps.

Reply

13 jsrt54 August 14, 2009 at 7:51 pm

Nice way of using the find syntax …

I did the same simulation using nested for loops and it generates the same results, with a tradeoff of the script being slower.

14 Krishna Sankar August 18, 2009 at 3:42 am: @jsrt54: Glad to hear.

Reply

15 Vini September 3, 2009 at 9:00 am

Using MATLAB, perform a Monte Carlo simulation of the four-level (quaternary) PAM communication system that employs a signal correlator.
• N = 10,000 transmitted symbols at different values of the average bit SNR
• Consider average bit SNR in the range of 0 to 12 dB.
• For convenience, normalize the distance parameter d = 1 and vary σ0.

I need the MATLAB graph please… I cant download MATLAB on my pc.. please help me someone… my due is tomoro… please…

16 Krishna Sankar September 8, 2009 at 5:50 am: @Vini: Please refer to the post on symbol error rate for 4-PAM simulations:
http://www.dsplog.com/2007/10/07/symbol-error-rate-for-pam/
If you dont have Matlab, you may download Octave and use.

Reply

17 cheri September 21, 2009 at 9:11 am

Can you advise me how I can stimulate the 8-PAM with a repeated input bit sequence of {101 000 100 101 100 100 100 011 001 100 110 110} , to produce the symbol error probability with less than 10^-4 ?

18 Krishna Sankar October 1, 2009 at 4:59 am: @cheri: You may start of with finding assign each bit groups to constellation points from [-7, -5, -3, -1, 1, 3 , 5, 7]/sqrt(21), and compute the bit error rate. For simplifying the simulations, try with zero noise and then later add noise. For high values of Eb/N0, you should be able to get BER less than 10^-4. Good luck.

Reply

19 N.A October 1, 2009 at 1:20 pm

could u please tell me the noise standard deviation for 8-PAM and the theoritical value of error probability of 8-PAM in AGWN channel?? thks before..

20 Krishna Sankar October 8, 2009 at 5:12 am: @N.A: Chapter 5.2.6 of Digital Communications by John Proakis, discuss the symbol error rate for a general M-PAM case. Plz check that out.

Reply

21 Richard October 12, 2009 at 6:12 am

i encoded my signal first with 5,2 block code and then converted to 4pam. I don’t know how to find the bit error rate or SER. can you please guide me?

22 Krishna Sankar October 13, 2009 at 4:54 am

@Richard: For finding the symbol error rate, compare the transmit and received constellation points. For computing BER, convert the received constellation into code bits, perform decoding and then compare the transmit and received bits. Good luck.

23 Richard November 12, 2009 at 4:15 am

What is the formula for theoretical value? I would like to find coding gain.
I saw a formula at your page:
http://www.commsdesign.com/article/printableArticle.jhtml?articleID=208802825
The formula is near the end of the article. Should I use that?

Thanks in advance.

24 Krishna Sankar November 13, 2009 at 5:37 am: @Richard: I have not assumed any coding in this writeup. Maybe I did not understand your query.

Reply

25 youcef November 13, 2009 at 5:37 am

Hi guys!
What happens if the messages are not equipropable???
I got a problem with defiining the thresholds.

26 Martin November 24, 2009 at 7:58 am

Hi,
Unfortunately, my mathematics got a little bit rusty. Could you help me with the step where you calculated p(e/s3)? I’m not sure how you got to the erfc() form –> First, the limits were “-inf” to “2*sqrt(Eb/5)”, than ” ” to “inf”. I tried to substitute as you did. –> z=y – sqrt(..) –> dz/dy=1 –> limits z=-inf -sqr() = -inf ….so its -inf , you ..you know. Additionally, how you got the N0 into the limits. Sorry, I really forgot how to do this. Orginally, I wanted to calculated the same as you did but with the Q() function.

Thanks,
Martin

27 Krishna Sankar December 7, 2009 at 4:20 am

@Martin: You can substitute z =(y – 3sqrt(Es/5))/sqrt(N0). With that substitution, the limits change from -Inf to 2sqrt(Es/5) to -Inf to -sqrt(Es/(5N0)). The latter is same integral from sqrt(Es/(5N0)) to Inf.
Agree?

28 Martin December 9, 2009 at 11:22 pm: Oh thank you. I forgot the sqrt(No). What a mistake.

Reply

Symbol Error Rate (SER) for 4-PAM

Channel Model

Computing the symbol error rate

Simulation Model

Reference

Related posts

Subscribe

Categories

Archives

Top Rated posts

Recent Posts

Comments

DSP

FPGA

General