In TETRA specifications, one of the modulation technique used is Differential 8 Phase Shift Keying (D8PSK). We will discuss the bit error rate with non-coherent demodulation of
D8PSK in Additive White Gaussian Noise (AWGN) channel.
pi/8 D8PSK
The incoming bit sequence is grouped into three bits and is mapped into differential phase as follows:
| B(3k-2) | B(3k-1) | B(3k) | |
| 0 | 0 | 0 | |
| 0 | 0 | 1 | |
| 1 | 0 | 1 | |
| 1 | 0 | 0 | |
| 0 | 1 | 0 | |
| 0 | 1 | 1 | |
| 1 | 1 | 1 | |
| 1 | 1 | 0 |
Table : Phase transitions for D8PSK modulation (Ref Table 5.2 of ETSI 301-893 V3.2.1)
The modulation symbol is formed by applying a phase offset to previous symbol
and is defined as follows:
and
.
Alternately, the phase transitions can be represented as
.
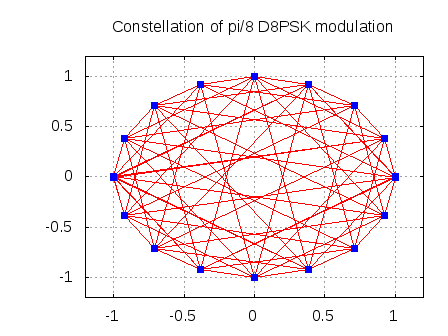
The constellation of the D8PSK occupies phase values separated by
as shown below in the blue dots. The red lines shows all possible phase transitions.
Figure: Constellation of D8PSK (Ref Figure 5.2 of ETSI 301-893 V3.2.1)
Channel Model
The transmitted waveform gets corrupted by noise , typically referred to as Additive White Gaussian Noise (AWGN).
Additive : As the noise gets ‘added’ (and not multiplied) to the received signal
White : The spectrum of the noise if flat for all frequencies.
Gaussian : The values of the noise follows the Gaussian probability distribution function,
with mean and
variance .
The received symbol is,
Non Coherent Receiver
A non-coherent receiver relies on the phase transitions between consecutive symbols to form an estimate of the transmitted bits. The sequence of operation is as follows:
a) On the received symbols estimate the phase
b) Find the delta of the estimated phase between consecutive symbols
c) Quantize the estimated delta phase values lying from as follows and convert to bits per the following encoding:
.
Simulation results
The script performs the following
(a) Generate random binary sequence of +1’s and 0’s.
(b) Group three bits together and apply D8PSK modulation
(c) Add white Gaussian noise.
(d) At the receiver, estimate the phase of the received symbols. Based on the delta of the received phase, estimate the transmitted bits
(e) Repeat for multiple values of and plot the simulation and theoretical results.
Click here to download the Script for computing BER for non coherent demodulation of pi/8 D8PSK in AWGN
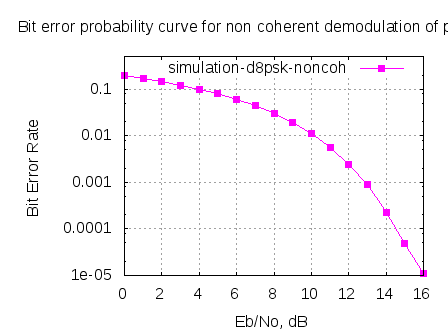
Figure: BER plot for D8PSK with non-coherent demodulation
Comments
As I did not find the theoretical BER equations for D8PSK, was unable to compare it with the simulated results.
I need new topic, please~~~
nice information. every student should follow. i personally suggest my students.
Great pieces of Information
@Hemant : Thanks, I reckon I know you 😉
just seen this blog no idea