Let us try to understand the formula for Channel Capacity with an Average Power Limitation, described in Section 25 of the landmark paper A Mathematical Theory for Communication, by Mr. Claude Shannon.
Further, the following writeup is based on Section 12.5.1 from Fundamentals of Communication Systems by John G. Proakis, Masoud Salehi
Simple example with voltage levels
Let us consider that we have two voltage sources:
(a) Signal source which can generate voltages in the range to
volts
(b) Noise source which can generate voltage levels to
volts.
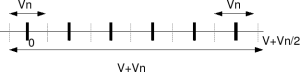
Figure: Discrete voltage levels with noise
Let us now try to send information at discrete voltage levels from the source (thick black lines as shown in the above figure). It is intuitive to guess that the receiver will be able to decode the received symbol correctly if the received signal lies within
.
So, the number of different discrete voltages levels (information) which can be sent, while ensuring error free communication is the total voltage level divided by the noise voltage level i.e.
.
Extending to Gaussian channel
Let us transmit randomly chosen discrete voltage levels
meeting the average power constraint,
, where
is the signal power.
The noise signal follows the Gaussian probability distribution function
with mean
and variance
.
The noise power is,
.
The average total (signal plus noise) voltage over symbols is
.
Similiarly, the average noise voltage over symbols is
.
Combining the above two equations, the number of different messages which can be ‘reliably transmitted‘ is,
.
Note:
1. The product of the signal and noise accumulated over many symbols average to zero, i.e
.
2. Since the noise is Gaussian distributed, the noise can theoretically go from to
. So the above result cannot ensure zero probability of error in receiver, but only arbitrarily small probability of error.
Converting to bits per transmission
With different messages, the number of bits which can be transmitted per transmission is,
bits/transmission.
Bringing bandwidth into the equation
Let us assume that the available bandwidth is .
Noise is of power spectral density spread over the bandwidth
. So the noise power in terms of power spectral density and bandwidth is,
.
From our previous post on transmit pulse shaping filter that minimum required bandwidth for transmitting symbols with symbol period is
Hz. Conversely, if the available bandwidth is
, the maximum symbol rate (transmissions per second) is
.
Multiplying the equation for bits per transmission with transmission per second of and replacing the noise term
, the capacity is
bits/second.
Voila! This is Shannon’s equation for capacity of band limited additive white Gaussian noise channel with an average transmit power constraint. 🙂
References
A Mathematical Theory for Communication, by Mr. Claude Shannon
[COMM-SYS-PROAKIS-SALEHI] Fundamentals of Communication Systems by John G. Proakis, Masoud Salehi
Hi,
Can someone explain this claim (Note 1 above)
“The product of the signal and noise accumulated over many symbols average to zero”.
Thanks
Nad
It means that noise and signal are independent. Since the mean of noise is zero
E[XY]=E[X]E[Y]=0
if X and Y are independent and E[Y]=0
@Abhishek: Thanks.
@nad: Hope that addressed your query
hi
i hope you are fine.please could you give me theoretical Bit Error Rate for convolutionaly coded BPSK,QPSK,16QAM,64QAM?please help me.
thank you.
@shadat: For BPSK with convolutional coding with hard/soft Viterbi, please refer to
https://dsplog.com/tag/viterbi
Please can u tell me how to change the data rate using spreading factor in matlab while using the same modulation scheme for different data rates.
BR,
Arif
AIT, Thailand
@Arif: Well, this depends on your simulation model. If you sampling rate is constant, but has a bigger spreading code, then the data rate reduce. Agree?
Hello…
consider 4 lvl system
thermometric – 000, 001, 011, 111 … 4 levels & 3 bits
coded as 2’s – 00, 01, 10, 11 …. 4 levels & 2 bits
quick look at the paper shows there is an assumption of coding in binary after some point, will read it later.
Chankaraaaa,
why is bits – messages related as log2(M)? if info is send as thermometric sequence will the no. of bits be = M / will the capacity linearly increase with snr for that case?
or suggest a good ref for me to understand these 🙂
@giri: Well, if a may bring in the analogy with ADC. With a k bit ADC one can split a voltage V into M=2^k regions, with each region is of width V/2^k (LSB size). Each message level can be positioned in the middle of each region with -LSB/2 to +LSB/2 on either sides as noise margin. So, if we assume that each message level can be used for transmission, then with M message levels we can have k = log2(M) bits 🙂 Makes sense?
Ofcourse, you can also look at the paper A Mathematical Theory for Communication, by Mr. Claude Shannon
Btw, what is a thermometric sequence?
@Jagan: Sorry, I do not have access to good personal lab.
If you wish, you can guest post a brief article on the new phase modulation scheme in dsplog.com. Further, I can forward the informtion to faculty of IISc, Bangalore (hopefully, after understanding your proposed scheme).
Hi Mr Pillai,
I saw your DSP Blog…and wishes to ask you a question.
Do you have access to a good lab, not just a matlab terminal?
I want to try out a new abrupt phase modulation scheme. I am based in California, SF bay area.
jagan