In the previous post on I-Q modulator and de-modulator, we had briefly mentioned that the a baseband PAM transmission can be modelled as
, where
is the symbol period,
is the symbol to transmit,
is the transmit filter,
is the symbol index and
is the output waveform.
In this post, the objective is to understand the properties of the transmit filter i.e. to find out a filter which occupies the minimum required bandwidth while ensuring inter-symbol-interference (ISI) free transmission of the information symbol
.
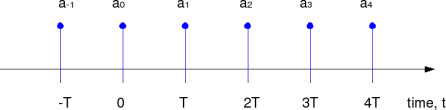
The sequence of transmit symbols maybe visualized as follows.
Figure: Transmit symbols for baseband PAM transmission
To recover the symbols from , one may sample the waveform at multiples of symbol interval
. The sampled waveform can be,
.
Breaking the above equation into two parts,
From the above equation, it is intuitive that for ensuring no inter symbol interference (ISI), the second term in the above equation should be zero i.e. the taps of the filter should be zero at
and non-zero at time
.
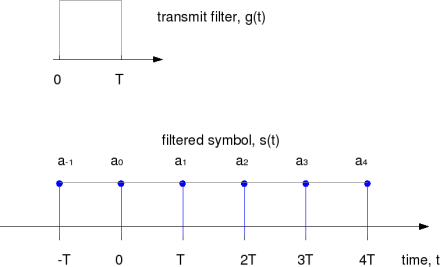
Rectangular filter
The most simplest filter is the zero-order hold filter, i.e. to repeat the current symbol till the next symbol arrives and so on. Mathematically, the filter can be represented as,
.
The filtered waveform can be as shown below.
Figure: Baseband PAM transmisison with rectangular filtering
Though there is no ISI with rectangular filtering, we will show later that this filtering is not be optimal from the bandwidth perspective.
Filtering with sinc() shaped pulses
From our textbooks, we may recall that sinc shaped pulses have have a band limited rectangular spectrum. For example, consider the sinc pulse of width .
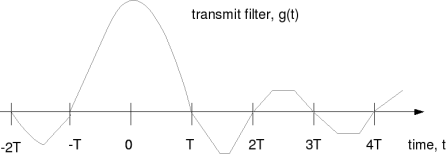
Figure: Time domain response of sinc filter
As desired, the above filter has zeros at and non-zero value at time
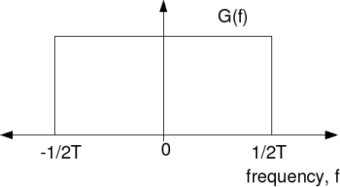
. The corresponding frequency response is a rectangular pulse bandlimited from
Hz to
Hz. The frequency response is as shown below:
Figure: Frequency response of sinc shaped filter
Infact, the above sinc shaped pulse satisfies the Nyquist criterion and is called Nyquist pulse (Refer Sec 5.1.1 [DIG-COMM-BARRY-LEE-MESSERSCHMITT]).
It follows that with the sinc shaped pulse (also called Nyquist pulse) used for transmit filtering:
(a) inter-symbol interference (ISI) is not introduced when sampled properly.
(b) minimum required bandwidth for transmitting symbols (with symbol period
)is
Hz.
Simulation model
Brief Matlab/Octave script for observing the spectrum of a random BPSK modulated symbols with rectangular filtering and sinc shape filtering might be helpful to uderstand the concept further.
Click here to download.
Matlab/Octave code for simulating transmit pulse shaping with rectangular and sinc waveforms
The observed spectrum is as shown below.
Figure: Transmit spectrum with rectangular and sinc shaped pulse shaping filter
Summary
1. From the above spectrum plot, the sinc shaped filter does not result in perfectly bandlimited spectrum from from Hz to
Hz. This is because, by theory, the sinc pulse exists from
to
. However, for simulations the sinc pulse is truncated for a finite duration. This results in negligible (less than -30dB) spectral content present outside
Hz.
2. The above discussion does not present why the sinc shaped filtering is optimal for ensuring minimum bandwidth. For the theoretical understanding, one may refer Sec 5.1.1 of [DIG-COMM-BARRY-LEE-MESSERSCHMITT].
Reference
[DIG-COMM-BARRY-LEE-MESSERSCHMITT] Digital Communication: Third Edition, by John R. Barry, Edward A. Lee, David G. Messerschmitt
Hope this helps.
Krishna

Dear All,
I want to build a “FIR Sinc Filter” so Kindly request for a guidance here. As we all know that sinc filter is given by “sin x/x”. So, I want to understand How I can get a sinc filter Impulse response & transfer function response here.
In my GUI I have edit boxes such as,
Fs- Sampling Frequency
Fc- Cutoff frequency
N- Filter Order
n- Input word length
CWL- coefficient Word Length
OWL-Output Word Length
I don’t want to use any window type at the moment, but want to build a basic ‘FIR Sinc filter’ and check the impulse & transfer function responses. So if I say,
Fs = 1000 (1KHz)
Fc = 400 (400Hz)
N = 20 (Filter Order)
n = 16 (16 Bit input word length)
CWL = 8 (8 Bit coefficient Word Length)
OWL = 16 (16 Bit Output Word Length)
How can one get a ‘FIR Sinc Filter’ for above parameters with ‘sin(x)/x’ ??
I want to access the coefficients of such a filter, but how??
You may find a High Pass Filter in the GUI I have but I want to include a ‘FIR SINC Filter’ in this GUI.
https://www.dropbox.com/s/q63m7e3q0yt8m8f/Sinc_Filter_Check.fig
https://www.dropbox.com/s/jd7mxtf1mtgdvor/Sinc_Filter_Check.m
Can any one guide me here ??
@Prashant:
Am hoping that this small matlab code snippet address your requirements.
To convert the coefficients to 8 bits (or N bits), do ht_fx = round(ht*2^N)/2^N;
Hope this helps.
% defining the filter coefficients
clear all; close all
nTap = 20;
fc=400;
fs = 1000;
ht = sin(pi*[-nTap/2:nTap/2-1]*2*fc/fs)./(pi*[-nTap/2:nTap/2-1]*2*fc/fs);
ht(nTap/2+1) = 1;
% plotting the freq response
hf = fft(ht,1024);
plot([-512:511]/1024*fs,20*log10(abs(fftshift(hf)))),’r’;
xlabel(‘freq, Hz’); ylabel(‘amplitude, dB’); grid on;
Dear Krishna,
there is a small error in your script, the sinc function is undefined there for t=0. This value shall be set to 1.
Regards
@joel: Thanks for noticing and reporting it. For some reason, my Octave version cleanly handles that case and outputs the value 1. Hence I missed it. I corrected it, anyways.
i have a question .plz ans me
how can i implement ICI and eliminate that in our OFDM system.
@Jamil: To model inter carrier interference (ICI) in an OFDM system, you may introduce frequency offset. The code in the post https://dsplog.com/2008/03/03/frequency-offset-estimation-using-80211a-short-preamble/ will hopefully provide you a reference for how to introduce carrier frequency offset.
Removing the effect of intercarrier interference after taking FFT is difficult (unless the effect of ICI is small). Else you may estimate carrier frequency offset in time domain and remove the effect of that in time domain itself prior to taking FFT.
Hope this helps.
I am a bit confused about oversampling. What is the difference between choosing carriers 52 (in OFDM) and FFT value 128 where I assume this is 2x oversampling and also the upsampling method you have here where you add zeros between samples. Do I misunderstand something here?
@Claire: Well both are oversampling, but there is no direct comparison between both the approaches. However, there is a nice time-frequency duality to understand.
With the 64pt FFT vs 128pt FFT case, its oversampling in frequency domain. If for example, we use only even subcarriers in a 128pt, then in time domain the first 64 samples at the o/p of 128pt iFFT will be same as the last 64 samples.
The other case, where we insert zeros between samples, is over sampling in time domain. If for example, we insert a zero between every samples and observe the spectrum, we can see that the same spectrum is repeated twice.
@giri: Well, for rect we cannot do -T to T, as it will cause ISI.
Any reason why sync is assumed for -T & +T & rect as 0 to T ? shouldn’t both be from -T to T or very close to that with first null at 1/2T in freq?
@umar: Well, the upsampling by N involves two steps
(a) first insert N-1 zeros between the samples, then
(b) pass the zero inserted samples through a filter.
The above lines capture step (a) i.e. inserting 9 zeros inbetween the samples.
Hi, i have a question about upsampling in your code.
amUpSampled = [am;zeros(fs-1,length(am))]
amU = amUpSampled(:).’
are these lines basically upsampling the symbols by factor of 10.
Regards,
umar
Oh! Wonderful job!
Very good and actual post.
Thx, your blog in my RSS reader now
@Yahia: hmm… I am not sure about your point on frequency cannot be tracked with upsampling factor of 2. I think the digital PLL should be able to track the frequency drifts. Let me think more and get back to you.
Thank you for your reply… I agree with you that most implementations use upsample ratio of 4. I guess that the reason for that to enable two levels of tracking [phase and frequency], if you upsample by 2 you will not be able to track the frequency drifts! Do you agree with me on this point?
Your answer provided a great help. In fact I did not know that the main reference for deciding the filter order is the mask specification. That makes sense now to me. Thank you
@Yahia:
Both the q’s are related. One of the typical design constraint will be transmit spectral mask specification. I would expect the designer to choose a reasonable filter length with a reasonable upsampling ratio to meet the transmit mask specification with adequate margin. Further thoughts:
1. Ideally one would want to have a high upsampling ratio, but is limited by practical considerations. Higher upsampling ratio means – DAC’s are clocked faster, the filter is clocked faster etc leading into hardware complexity. Typical upsampling ratio I ve seen is around 4x the symbol rate. Typically this should enable us to achieve adequate rejection of aliases with a reasonable filter length.
2. As expected, more the filter length, better the rejection of aliases. However more taps means higher hardware complexity. As mentioned, above we may chose a filter sufficient to meet the mask with margin.
Helps?
I have two questions!
1- How do we decide the upsampling ratio before pulse shaping filter?
2- How do we decide the length of pulse shape filter?
hi friends. i want to design low pass multi stage raised cosine filter. how to design multi stage filter with raised cosine response. filter specification are:
sampling frequency = 15.36 MHz
rolloff factor = 0.22
cuttoff frequency = 3.84 MHz
passband frequency = 4.5 MHz
please tell me how to design.
@kiran: You may use the command rcosflt() in Matlab
http://www.mathworks.com/access/helpdesk/help/toolbox/comm/ref/rcosflt.html