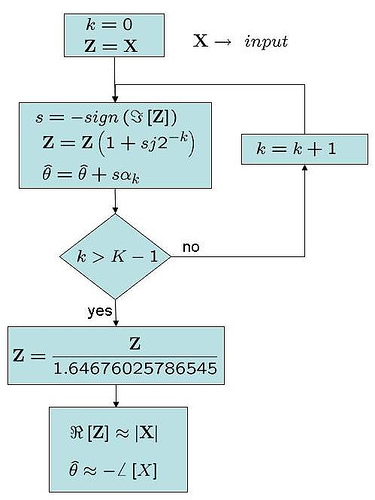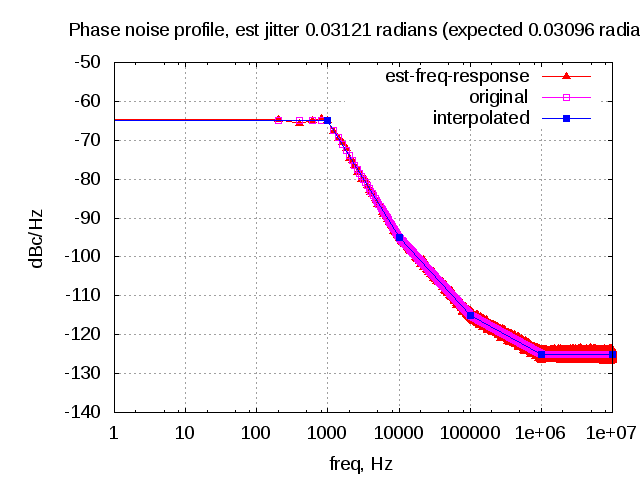
Modeling phase noise (frequency domain approach)
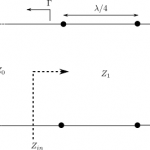
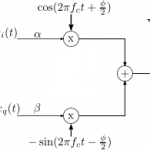
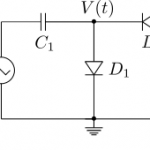
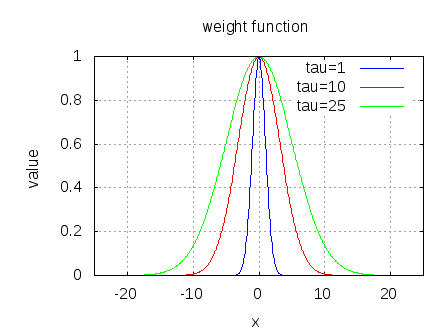
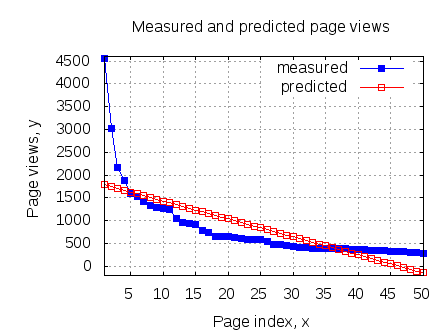
In typical wireless system simulations, there is a need to model the phase noise profile of the local oscillator. For eg, the phase noise profile of the oscillator can be of the shape described in the post on Phase Noise Power Spectral Density to Jitter. While looking around for example Matlab code, found two references…