CORDIC for phase rotation

My understanding of the CORDIC (Co-ordinate Rotation by DIgital Computer) thanks to the nice article in [DSPGURU-CORDIC].

The idea is that rotation of a complex number by an angle can be achieved without using multipliers. The phase angle is approximately equal to successive addition or subtraction of angles from a set of reference angles i.e. , where

,

is the set of reference angles,

is the sign (takes +1 or -1) and

is the number of iteration.

Let the complex number corresponding to reference phase is . The reference angles for different values of is listed in the table below

	Re{Y}	Im{Y} =	(in degrees)	abs()
0	1	1.000000000	45.000000000	1.414213562
1	1	0.500000000	26.565051177	1.118033989
2	1	0.250000000	14.036243468	1.030776406
3	1	0.125000000	7.125016349	1.007782219
4	1	0.062500000	3.576334375	1.001951221
5	1	0.031250000	1.789910608	1.000488162
6	1	0.015625000	0.895173710	1.000122063
7	1	0.007812500	0.447614171	1.000030517
8	1	0.003906250	0.223810500	1.000007629
9	1	0.001953125	0.111905677	1.000001907
….

Table: List of for = 1 to 10

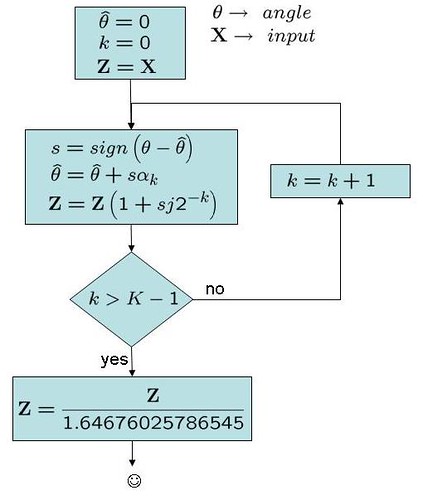
The set of operations for rotating a complex number by an angle to generate in the CORDIC way can be as shown below:

Figure: CORDIC for phase rotation

As the multiplication by involves only power of two, the operation can be implemented with out using ‘real’ multipliers. Nice advantage when we need to save hardware. The flip side is the number of iterations required for obtaining accurate estimate.

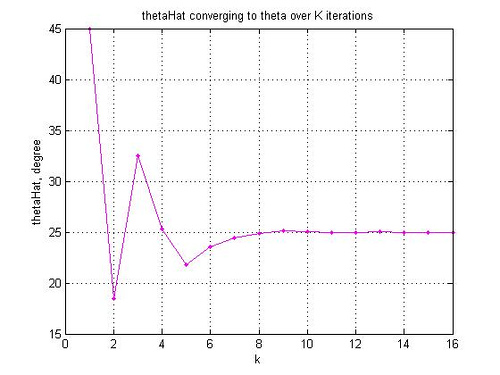
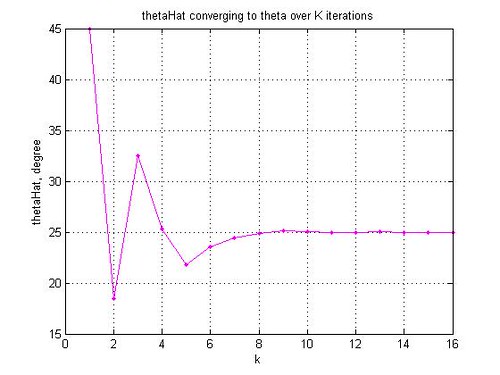
Additionally, the multiplication by introduces gain (as shown in the Table above) and after 16 iterations () the cumulative gain come to 1.64676025786545. Hence the block for compensating the gain.

% Simple Matlab example of phase rotation using CORDIC
clear
% creating the reference angles
Y_k = ones(32,1) + j*2.^(-1*[0:1:31])’; % values of Y
alpha_k = angle(Y_k)*180/pi; % reference angles

X = 2+3*j; % complex number to be phase rotated
thetaDeg = 25; % the phase to be rotated
K = 16; % number of iterations

thetaHat = 0; % initial phase angle
Z = X; % assigning the output as the input

% for different values of k
for k = 0: K-1
s = sign(thetaDeg – thetaHat); % difference
if s == 0 s = 1; end % to handle when thetaDeg = 0
Z = Z*[1 + s*j*2^(-1*k)];
thetaHat = thetaHat + s*alpha_k(k+1);
% dumping the variables for plot
sign_v(k+1) = s;
thetaHat_v(k+1) = thetaHat;
end

Z_ideal = X*exp(j*thetaDeg*pi/180);
Z_cordic = Z/1.64676025786545;
err = Z_ideal – Z_cordic;
errdB = 10*log10(err*err’)

close all
figure
plot(thetaHat_v,’m.-‘)
grid on
xlabel(‘k’)
ylabel(‘thetaHat, degree’)
title(‘thetaHat converging to theta over K iterations’)

Reference

[DSPGURU-CORDIC] CORDIC FAQ in dspGuru(TM)