GATE-2012 ECE Q24 (math)

Question 24 on math from GATE (Graduate Aptitude Test in Engineering) 2012 Electronics and Communication Engineering paper.

Q24. Two independent random variables X and Y are uniformly distributed in the interval [-1, 1]. The probability that max[X,Y] is less than 1/2 is

(A) 3/4

(B) 9/16

(C) 1/4

(D) 2/3

Solution

Let

.

Expanding,

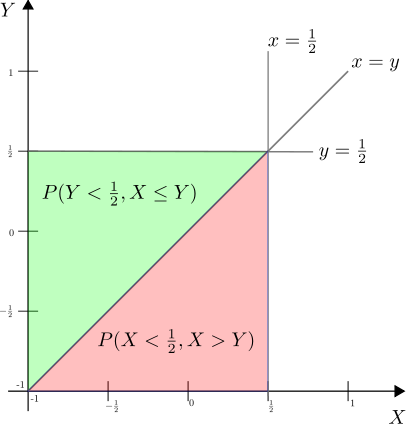
The above equation can be represented as shown in the figure below and the total probability is the sum of green and red regions.

The sum of red and green regions is

.

Since and are independent,

.

From probability density function of uniform random variable,

.

Summarizing, the total probability is

.

Matlab example

clear all;
N    = 10^5;
x    = 2*rand(1,N)-1; % uniform distributed [-1,1]
y    = 2*rand(1,N)-1; % uniform distributed [-1,1]
prob = size(find(max(x,y)<1/2),2)/N

Based on the above, the right choice is (B) 9/16

References

[1] GATE Examination Question Papers [Previous Years] from Indian Institute of Technology, Madras http://gate.iitm.ac.in/gateqps/2012/ec.pdf

[2] Wiki entry on Uniform random variables

http://en.wikipedia.org/wiki/Uniform_distribution_(continuous)

[3] Function of two random variables, notes from Caltech

http://ee162.caltech.edu/notes/lect8.pdf