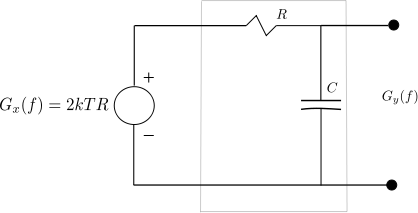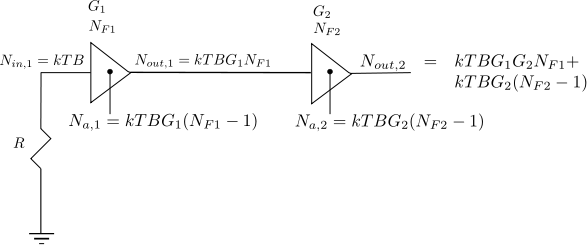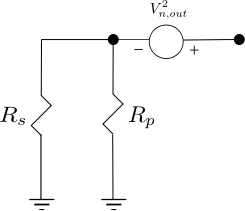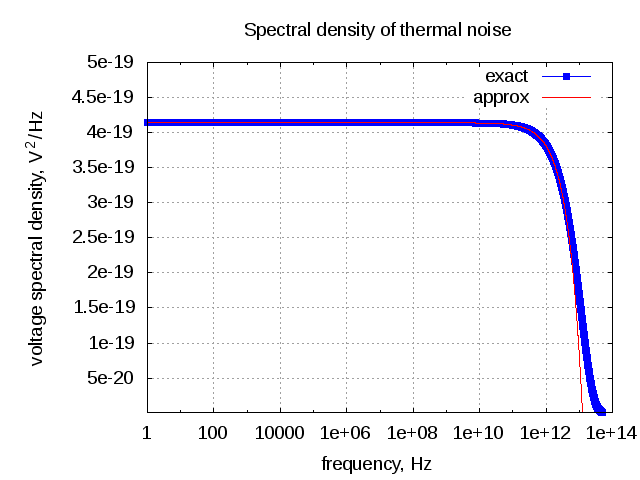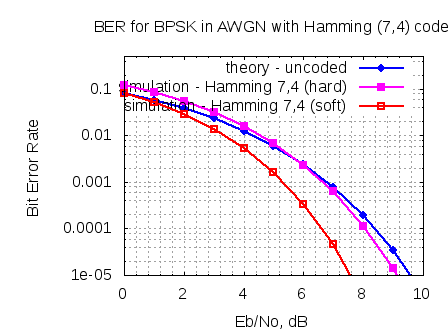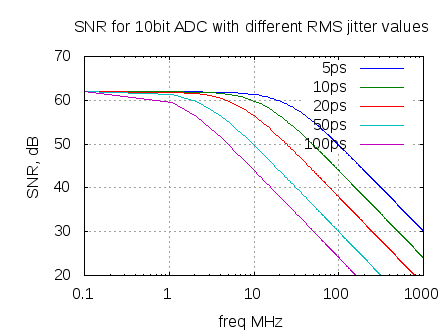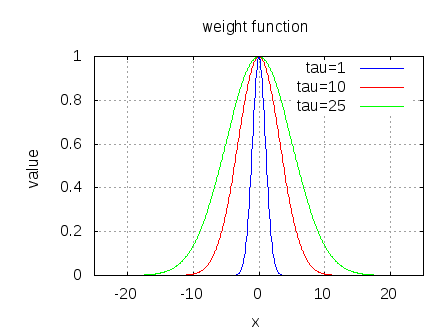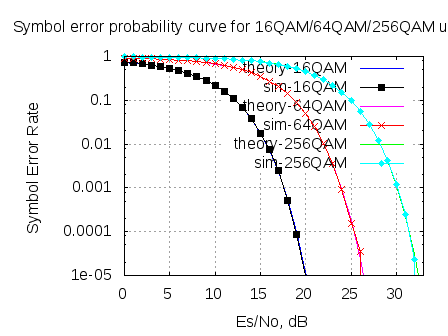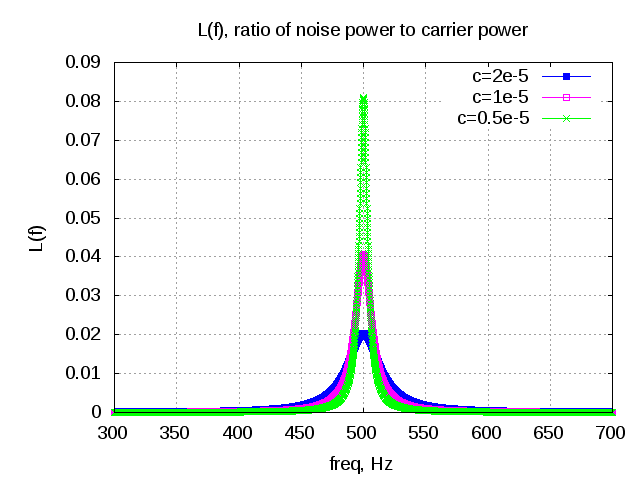
Oscillator phase noise
Oscillators are used in typical radio circuits to drive the mixer used for the up-conversion or down-conversion of the passband transmission. Ideally, the spectrum of the oscillator is expected to have an impulse at the frequency of oscillation with no frequency components else where. However the spectrum of practical oscillators do have spectrum skirts around…