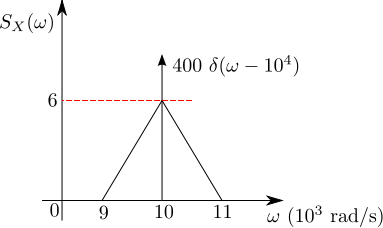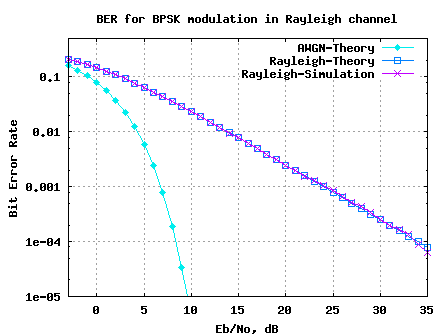
BER for BPSK in Rayleigh channel
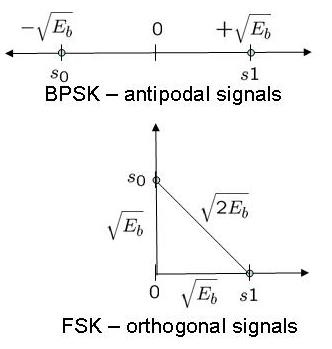
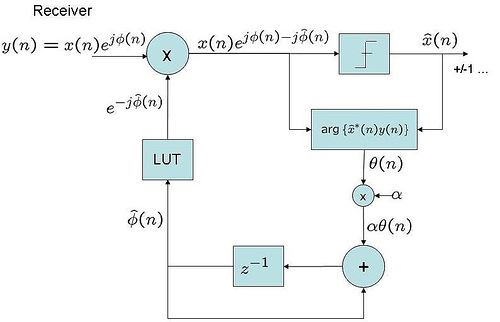
Long back in time we discussed the BER (bit error rate) for BPSK modulation in a simple AWGN channel (time stamps states August 2007). Almost an year back! It high time we discuss the BER for BPSK in a Rayleigh multipath channel. In a brief discussion on Rayleigh channel, wherein we stated that a circularly…