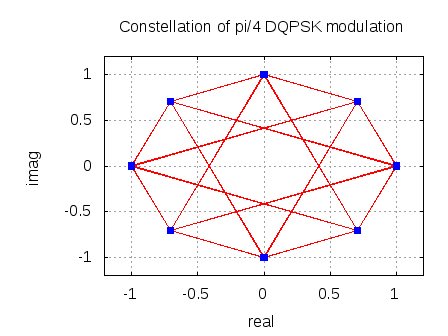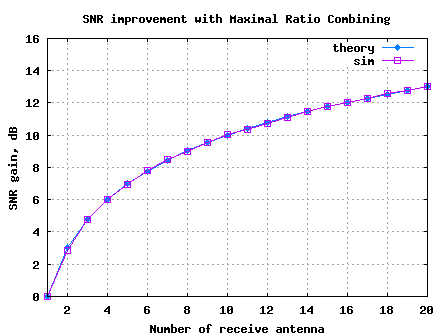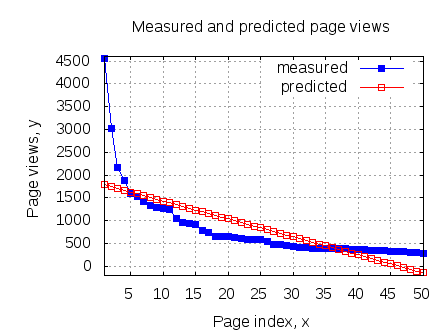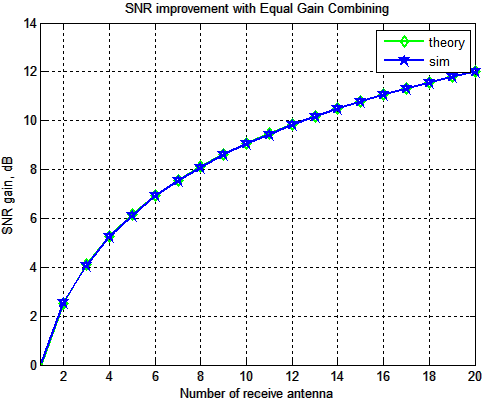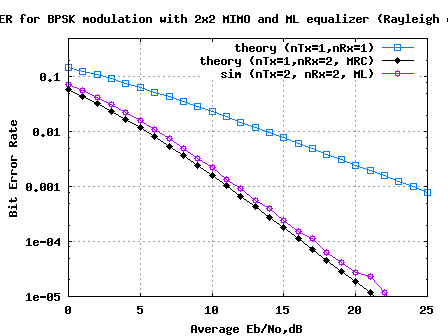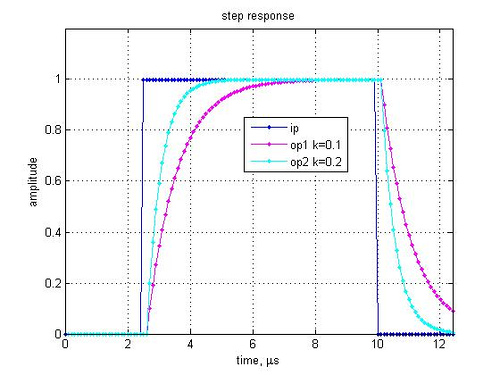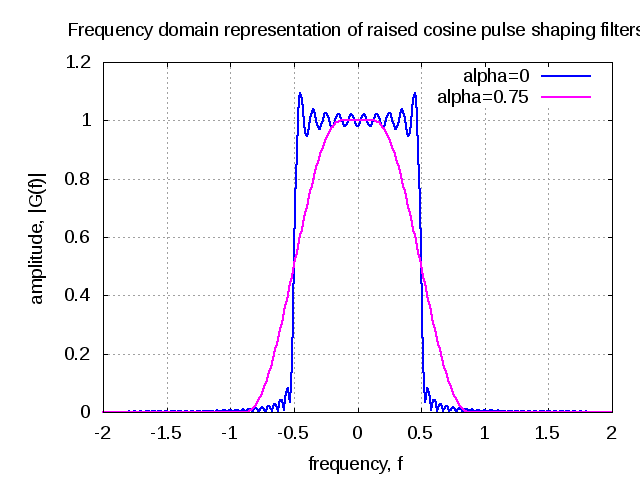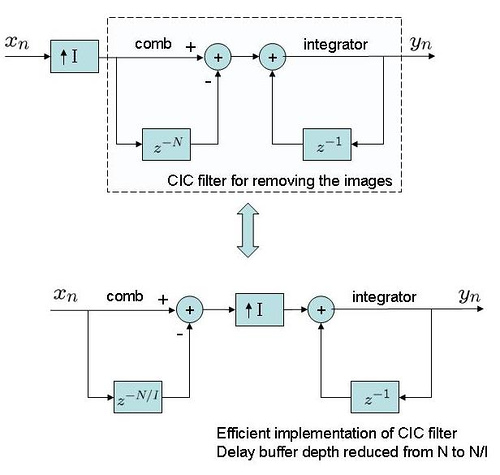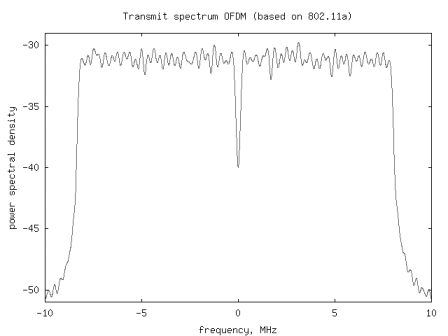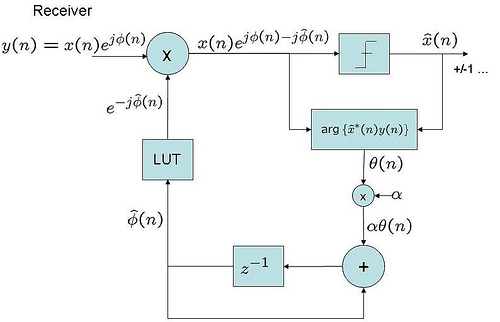
First order digital PLL for tracking constant phase offset
Considering a typical scenario where there might exist a small phase offset between local oscillator between the transmitter and receiver. Figure 1 : Transmitter receiver with constant phase offset In such cases, it might be desirable to estimate and track the phase offset such that the performance of the receiver does not degrade.