Straight line fit using least squares estimate
Two points suffice for drawing a straight line. However we may be presented with a set of data points (more than two?) presumably forming a straight line. How can one use the available set of data points to draw a straight line?
A probable approach is to draw a straight line which hopefully minimizes the error between the observed data points and estimated straight line.
where
is the observed data points and
is the points from estimated straight line.
To draw the estimated straight line , we need to estimate the slope,
and the constant,
.
Formulating as a matrix,
,
where,
=
is the set of observations is a matrix of dimension
,
=
is the set of coefficients is a matrix of dimension
,
is the slope and constant estimate of dimension
,
=
is the noise is a matrix of dimension
.
The least square estimate of the straight line is,
.
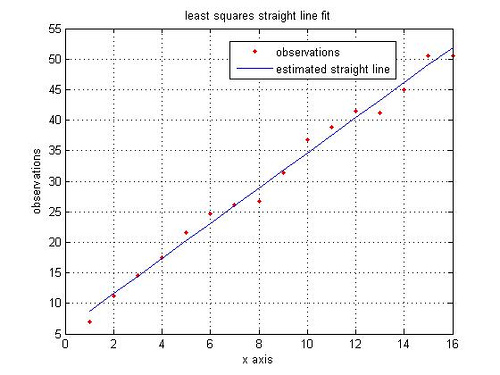
A simple MATLAB code for least squares straight line fit is given below:
% Least Squares Estimate
rand(’state’,100); % initializing the random number generation
y = [5:3:50]; % observations, y_i
y = y + 5*rand(size(y)); % y_i with noise added
x = 1:length(y); % the x co-ordinates
% Formulating in matrix for solving for least squares estimate
Y = y.’;
X = [x.' ones(1,length(x)).'];
alpha = inv(X’*X)*X’*Y; % solving for m and c
% constructing the straight line using the estimated slope and constant
yEst = alpha(1)*x + alpha(2);
close all
figure
plot(x,y,’r.’)
hold on
plot(x,yEst,’b')
legend(’observations’, ‘estimated straight line’)
grid on
ylabel(’observations’)
xlabel(’x axis’)
title(’least squares straight line fit’)
References:
[1] Details on Curve fitting toolbox from MathWorks(TM) website
Please click here to SUBSCRIBE to newsletter and download the FREE e-Book on probability of error in AWGN. Thanks for visiting! Happy learning.
(No Ratings Yet)
Loading ...If you liked this post, you may leave a comment below, or subscribe to the RSS feed.
You may also find these posts relevant...
Comments
No special reason, except that when does this way, I have a reasonably clear idea of the underlying operations. Maybe helpful if I want to implement.
For the example above, the least squares solution can be obtained either by using X\Y or pinv(X)*Y. However, when X is rank-deficient, then the code in the post may fail and more ‘intelligent’ operations X\Y or pinv(X)*Y might be needed.
And a quick check showed that \ operator runs faster than pinv() or the code in the post.
Additionally, a nice thread in comp.dsp on this topic maybe interesting.
From the Data given below fit a straight line trend by the methord if least square and also estimate the sales for the year 1984.
Year 1971 1976 1977 1978 1979 1980 1981 1982
Sales 6.7 5.3 4.3 6.1 5.6 7.9 5.8 6.1
I find it interesting that you used inv and performed the matrix multiplication to solve this problem. Do you have a reason for doing it this way, instead of using MATLAB’s backslash operator (as in the linked material, below)?
Linear Regression in MATLAB
In curiosity,
Will