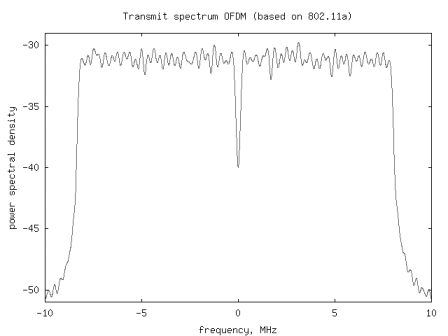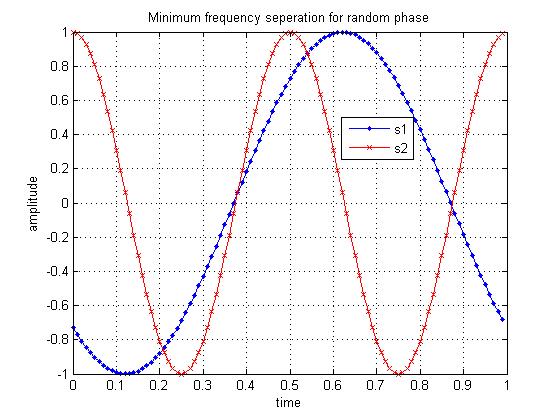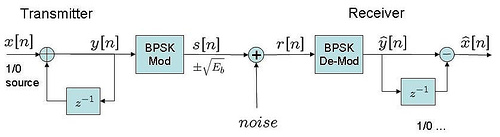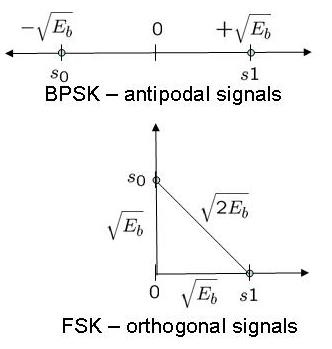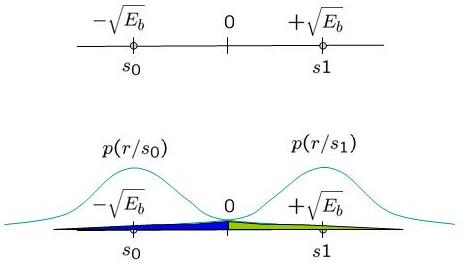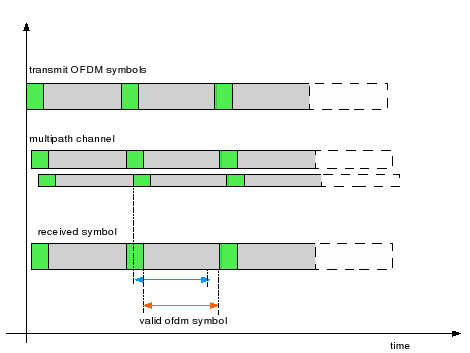
Cylcic prefix in Orthogonal Frequency Division Multiplexing
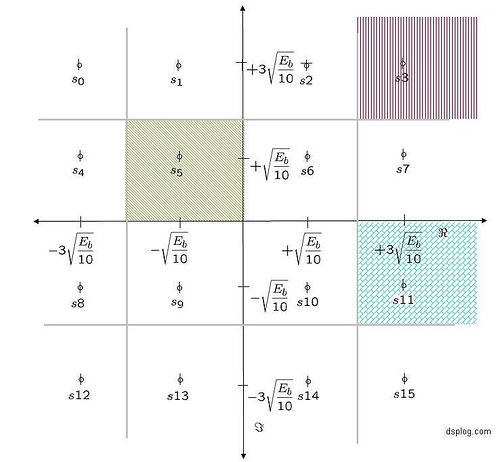
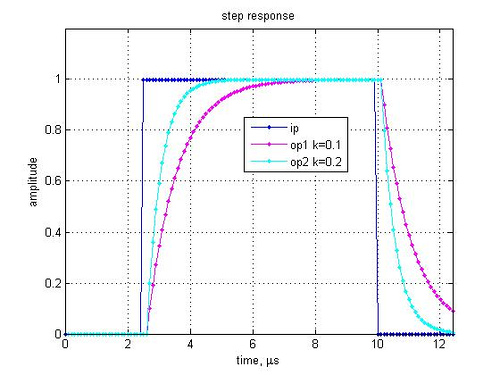
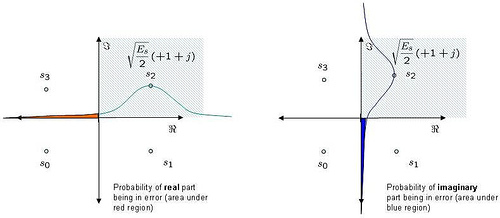
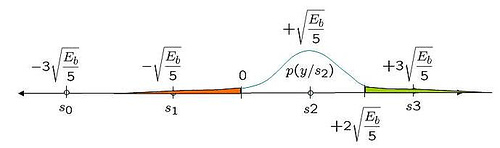
In a previous post (here), we discussed in brief, Orthogonal Frequency Division Multiplexing (OFDM) transmission. Let us know probe bit more into the motivation of cyclic prefix (aka guard interval) associated with each OFDM symbol. What is cyclic prefix? Let us consider one subcarrier (subcarrier +1 specified in IEEE 802.11a specification) alone. In the figure…