When QAM (Quadrature Amplitude Modulation) is used, typically one may find a scaling factor associated with the constellation mapping operation. It may be reasonably obvious that this scaling factor is for normalizing the average energy to one.
This post attempts to compute the average energy of the 16-QAM, 64-QAM and M-QAM constellation (where is a power of 2), thanks to the nice example 5.16 in [DIG-COMM-BARRY-LEE-MESSERSCHMITT]
.
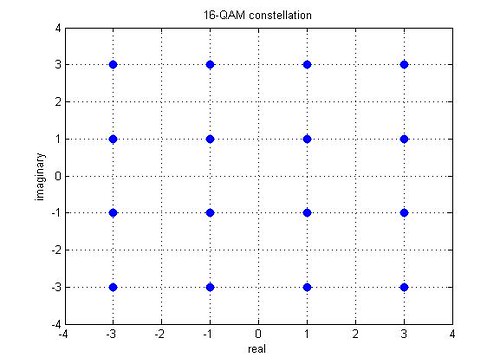
Consider a typical 16-QAM modulation scheme where the alphabets
are used.
Figure: 16QAM constellation mapping
Observations:
1. The number/type of the used constellation points in all the four quadrants are similar. Hence average energy computed over one quadrant is same as the energy over all the quadrants. The mean power can be computed over 16/4 = 4 constellation points.
2. The same alphabet set is used for real and imaginary axis. Hence energy of real and imaginary components are the same.
3. In each quadrant, the elements of each alphabet is used times by real and imaginary part respectively.
Considering so the average energy of 16-QAM is,
.
Hence the constellation points of 16-QAM are normalized with the factor to ensure that the average energy over all symbols is one.
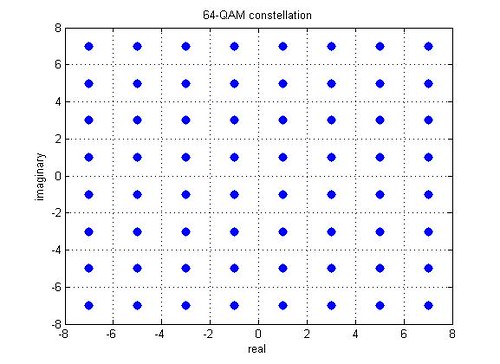
Consider a 64-QAM modulation scheme with the alphabets
.
Figure: 64QAM constellation mapping
Observations for 64-QAM:
1. Each quadrant has 16 constellation points
2. The energy of real and imaginary components are the same.
3. In each quadrant, the elements of each alphabet is used times by real and imaginary part respectively.
Hence the constellation points of 64-QAM are normalized with the factor to ensure that the average energy over all symbols is one.
Extending this to a general M-QAM constellation mapping, where is a power of 2. The elements of the alphabet are
, where
.
1. Each quadrant has constellation points
2. The energy of real and imaginary components are the same.
3. In each quadrant, the elements of each alphabet is used times by real and imaginary part respectively.
.
% Simple Matlab example
% QAM scaling factor
clear
clc
alpha_16qam = [-3 -1 1 3];
N = 10^5;
const_16qam = randsrc(1,N,alpha_16qam) + j*randsrc(1,N,alpha_16qam); % generating 16-QAM constellation points
energy_16qam = const_16qam*const_16qam’/N
alpha_64qam = [-7 -5 -3 -1 1 3 5 7];
const_64qam = randsrc(1,N,alpha_64qam) + j*randsrc(1,N,alpha_64qam); % generating 16-QAM constellation points
energy_64qam = const_64qam*const_64qam’/N
Can observe that energy_16qam and energy_64qam takes values close to 10 and 42 respectively.
Hope this helps.
Krishna
Reference
[DIG-COMM-BARRY-LEE-MESSERSCHMITT] Digital Communication: Third Edition, by John R. Barry, Edward A. Lee, David G. Messerschmitt
Hello Krishna,
I went through your code for SNR – BER plot for 16 QAM using gray code mapping. I wanted to know the input alphaRe = [-3,-1,1,3 ] gives 2 dimensional QAM constellation Could you please tell how can I get 16 QAM in 3 dimension using this code..?
Thanks a ton.
@Priyanka: 3 dimension – did not understand. can you please clarify
I mean 3 dimension signal constellation of 16 QAM. If QAM is given as,
s(t) = A*cos(2pi*f1*t)+ Bcos(2pi*f2*t)+ C*cos(2pi*f1*t)
then can we use this code for [-1,1] of A,B,C values…?
Thanks.
@Priyanka: Hmm.. but, A and C are sent on the frequency f1. How will you be able to independently recover A and C from the combined signal?
Ohh sorry C has frequency f3 not f1. All three signals A,B, C have different frequencies..
@Priyanka: So, this is the case of sending independent information on three frequencies. Am hoping that these 3 frequencies are orthogonal to each other. Load some arbitrary values from the 16-qam constellation to the 3 subcarriers.
Hi Krishna..thanks for your posts. Can you please elaborate that why do we need to make the transmit power to unity . Has it got something related to noise power..lemme know,,thanks
@Abhijit: The transmit power is made to unity to help make a fair comparison while comparing different modulation/coding schemes.
Hi Krishna,
During simulations for my research paper, I was left wondering about the correlation matrix R = E[x x^H] for a QAM constellation. For QPSK, it’s straightforward enough, since after scaling, each symbol has unit energy, the average energy is 1 and R = I. Initially I thought that for QAM, it would be a scaled identity matrix with different diagonal values.
I was trying to ascertain this on the web when I came upon your article.
After looking at your matlab code for QAM scaling factor above, where you
have showed that the experimental average of the symbols is close to the theoretical
average, it struck me that a similar thing happens to the correlation matrix, resulting
in a diagonal matrix with equal diagonal values, and this value is the average energy in the constellation.
May I add that the artcile is very well written. Thanks.
@Prasad: Thanks
Hi Krishna,
Okay, that makes sense. And how is scaling the voltage equals to scaling the power to unity? I am sorry, I am quite lost here.. Maybe you could refer the mathematical relation, that will help me to see it… Thank you Krishna.
@Aiyu: Hmm… power ~= voltage^2.
Hi Krishna, thank you for explaining for to normalize the average energy/symbol to one.
I get that energy of 16QAM =10, now this might be silly but I don’t get why is it scaled by sqrt(10) instead of 10 to get energy/symbol=1 ???
thank you
@Aiyu: The factor 1/10 is to scale the energy. Correspondingly the voltage signal is scaled by 1/sqrt(10).
Helps?
Hello Krishna,,,
Thanks for useful article. Can you please guide me for normalization of ofdm signal. I’m simulating a bandpass ofdm signal but it gives me more bit error rate which is greater than the theoretcal one. For a baseband ofdm it works fine. I’m wondering how would i normalize noise, which is for real valued signal only,,,,
Thanks
@Mishaal: Are you seeing a 3dB difference?
Hi,
I need the Matlab code example for simulation of BER vs SNR for M-ary 64QAM.
Could you help me?
regards,
Hassan
@Hassan: I have a post on 16 QAM Bit Error Rate @ https://dsplog.com/2008/06/05/16qam-bit-error-gray-mapping
Hope that helps.
Thank you very much! It’s really helpful!
Mr K.Pillai,
I first of all want to appreciate the immense knowledge i have gain since a friend introduced me to dsplog.
I have an urgent problem i need to sort out.I desperetely need you to help me on this the way you have conviniently help peopl out.
1.I need a matlab code to run a clear case scenirio in satellite channel channel with figures displaying 16qam constellation,eb/no
2.A matlab code to generate rain or any fade event with display on the the efect on eb/no or ber and constallation of qam shown.
3.Then code to mitigate the fades ,so that a good link is achieved.
we have site dievrsity,power control and adaptive waveform as the basic three mitigations.
hope to hear from you soon.
@Muhammad: Though I do not have the specific posts which you are looking for, https://dsplog.com/tag/qam/ might be of help.
krishna… plz tell me how we can mitigate the effects of phase noise in OFDM systems…
@Asma: Well, typical OFDM symbols will have pilots interspaced between data symbols. We need to estimate the phase from the pilots and compensate prior to demodulation.
dear mr krishna
may i know,how we determine the number of symbols,N at the beginnign of the code?why every modulation has different kind of N?thanks
@rashid: The total number of symbols N is chosen to make the simulation statistically accurate. It does not depend too much on the modulation type
How about the matlab script for 8qam and 32 qam??
Ok..thanks Krishna…
How about the constellation diagram for 8QAM and 32QAM??
Hi Mr.Krishna
please help me,,
Can you tell me How to show picture of signal for 8 QAM,16 QAM and 32 QAM in matlab6.1?
And Then How about the constellation diagram for 8 QAM, 16QAM and 32 QAM in matlab 6.1?
@reeda: Let me give an example matlab script for 16qam
>>clear all; close all
>> alpha_16qam = [-3+-3*j, -3+-1*j, -3+1*j, -3+3*j, -1-3*j,-1+-1*j,-1+1*j, -1+3*j, 1+-3*j,1-1*j,1+1*j, 1+3*j, 3+-3*j,3+-1*j,3+1*j, 3+3*j];
>> plot(real(alpha_16qam),imag(alpha_16qam),’bs’)
>> axis([-4 4 -4 4])
How about with Truth table of 32 QAM?
@reeda: Truth table for 32QAM? Sorry, I did not understand your query
hello! Krishina
please help me my project is OQAM\ofdm but i cant find any code or tutorial document in the web or your website??
Thank you advance
behzad
@Behzad: I have discussed about OFDM. You may find articles in https://dsplog.com/tag/ofdm
I have not discussed much about OQAM. The closest which I have come is to discuss MSK which is a variant of OQPSK.
https://dsplog.com/2009/06/16/msk-transmitter-receiver/
sir,
can you tell me , how to know frequency of qam signal by using ‘qammod’ command in matlab… OR how to know the frquency of the QAM signal that is being transmitted by using MATLAB programme.
@prabin bera: The concept of frequency in matlab is notional. One can define the time gap between the samples based on the simulation needs. For eg, if we have a sequence [1 2 3 4 5 ], the gap between 1 and 2 can be 1 second or 1us or any other value which we choose.
I am new in the normalization process and I don’t understand the purpose of it. I’ve been told that I should use normalization when I want to compare different qam systems. Is this correct? I don’t understand what the actual achievement and benefit is when normalizing the average energy to one.
In one of the previous posts you mentioned that using normalization does affect the ber of a system, and I also found out that the normalised system has a worst performance than the non-normalised. So my question is why to deteriorate a system just for comparison purposes.
Obviously there is something I am missing out and I would be grateful to you if you could point that out.
Your response will be greatly appreciated.
Thank you advance,
Vassilis
@vassilis: My replies
1/ Yes, normalization is used to compare different systems.
2/ Lets say, me and you are competitors building a wireless communication transmitter. To make a fair comparison on who has the higher range, we should make both your’s and my transmitter to have the same transmit power and then check the range. Makes sense?
3/ In the simulation model, we need to define the SNR correctly to get the simulated bit error rate to be equal to theoretical bit error rate. That can be achieved by scaling the transmit signal or noise signal or both.
hello! Krishina . Iwould like you to ask a help concerning 16-QAM modulation technique. I doing a matlab simulation for 16,64-QAM ,2 channels for (eg 16qam 2bits which MSB in one channel and 2bits LSB in other ) i did that without noramlization and it’s working fine but when i did that with normalization didn’t get the exact output, do you have a matlab script which is used to simulate performance(BER,SER Vs SNR) of 16 or 64-QAM modulation technique. Or shell i send my script to you to cheek.
Thanks….
Thank you inadvance
@ahmed: Sorry, due to time constraints may I refuse to debug the code. You may look at
https://dsplog.com/2007/12/09/symbol-error-rate-for-16-qam/
Hi Krishna .
If we don’t use the normalzation is the simulation results wrong? Because i use 16qam , 64qam and 256qam and i partitioning the data according to the modulation channels in 2 channels high priority(HP) and low priority (LP) so MSB to HP and LSB into LP . I found lots of papers related to my work without normalization. So please could advice me.
Thanks
@ahmed: Well, to get our reference curves right, we need to get simulation results comparable to theoretical curves.
Dear Khrisna.
Am trying to run this program but the tradoff unaccaptable could you please indict me to my mistake.
clear all;
close all;
M = 16;
k=log2(M);
n=5e4;
x=randint(n,1,M);
inphase =[ 1; 1; 3; 3; 3; 3; 1; 1; -3; -3; -1; -1; -3; -3; -1;-1];
quadr =[ 1;3;1; 3; -3; -1; -3; -1; 3; 1; 3; 1; -3; -1; -3; -1];
nor=1/(sqrt(10)); % normalization
const = inphase + j*quadr;
y=genqammod(x,const); % modulation
y1=y*nor;
scatterplot(y1);
ebnodb=-5:15;
for i=1:length(ebnodb);
ebno(i)=10^(ebnodb(i)/10); % energy per bit
esno(i)=ebno(i)*k;%convert ebno to esbo
es=10;
noise_var=es/esno(i)*(1/2);
noise_std=sqrt(noise_var);
n_i=randn(length(y1),1)*noise_std;
n_q=randn(length(y1),1)*noise_std;
noise=n_i+j*n_q;
ynoise=y1+noise;
ynoise1=ynoise/nor;
z=genqamdemod(ynoise1,cost); % demodulation
[ber_num,ber_ratio(i)]=symerr(x,z);
end
figure
semilogy(ebnodb,ber_ratio);
@ahmed: Sorry, I do not have the functions genqammod/demod()
Hi Krishna I have one question regarding normalization. Is the normalization effect the bit error rate?
Thanks
@ahmed: Normalization is used to make the transmit power to unity. Yes, it will affect the bit error rate.
Dear Khrisna,
I have tried the simulation to normalize the power of QPSK but it did not work. I generated the constellations and then i multiplied them with the factor of 1/sqrt(2), the last step, i calculated the power by multiplying the normalized constellations with the conjugates, but it did not result unity. Was i wrong? thanks
@Leni: With QPSK it should be simple. For eg, assume only one constellation point
>>c = (1+j)/sqrt(2);
>> c*conj(c)
ans = 1.00000
Did you take the mean of the samples?
@Krishna
Hi Krishna I have one question regarding the 16 QAM signal.
If the average energy of a 16-QAM signal is 1, what is the distance between two adjacent points in its signal space diagram?
it is sqrt (10). or 1/sqrt(10).
Please reply asap.
Thanks
@kirtesh vora: The distance between adjacent constellation points in 16-QAM is 2/sqrt(10). 🙂
Note: The factor 1/sqrt(10) is to normalize the power to unity.
@Krishna:
For non-square constellations it would be better first to compute the total energy for the larger square(including the gap at a corner) and then subtracting the energy for the gap.
Rest of the procedure same.
(Just by observation it seems it is also possible to find a more generic & graceful method)
@Jagadeesh: Yes, thanks 🙂 I was further wondering whether we can find a generic equation based on geometry (have not thought about it yet).
@Tahmid: Sorry, I did not look at the non-square constellation normalization. I hope to revert with in couple of days.
Hi Krishna,
Following on from you last comment on this page, did you manage to find normalizing factor for rectangular constellations such as 8QAM, 32QAM?
thanks. I am learning so much from your contributions!
@Guenter: Indeed, you are correct. There was a typo and it should have read 2/3*(M-1). I corrected the same.
For the rectangular constellation (where sqrt(M) is not a power of 2), I do not recall reading a simple formula in the literature. One way might be to find the power of the square constellation present in the structure and then add the power from the remaining constellation points.
Anyhow, let me have a look.
Thanks for that example, I have been searching the web a long time to find something about constellation scaling.
Concerning the formula for E_MQAM I believe there is a small typo. It should be 2/3*(M-1) instead of 2/3*M-1. I think you even said that in one of the later comments.
How would you go about constellations of sizes where sqrt(M) is not a power of 2? Is there an easy way to derive a formula for that?
@umar:
Typically, we will be using the channel model to find out the packet error rate for each value of SNR. The normalizing factor in the channel model ensures that the resultant average SNR after passing through the channel is same as the defined SNR. Makes sense?
Hi, I think this is the first time i have understood why we require to multiply a scaling factor to our signal.Cheers for that.
I would request you to please eloborate a bit as to why we require to normallize the power in a channel as well. say if a channel is 6 taps (complex) than we are require to multiply it with 1/sqrt(6). or i can put my question in more general term and ask why we want that equivalent taps in all channels have equal power.
Regards,
umar
Thank you so much Krishna!
@ali:
well, i looked at pammod() and qammod(). Seems it does not do the normalization. You either need to normalize manually (as we know the number apriori) OR you can use the function modnorm()
Maybe the script which is extracted from ‘help modnorm’ is useful.
M = 4; % M-ary number.
const = pammod([0:M-1],M); % Generate a constellation.
s = randint(1,100,[0 M-1]); % Random signal
Scale = modnorm(const,’avpow’,1); % Compute scale factor for an
% average power of 1 watt.
Tx = Scale * pammod(s,M); % Modulate and scale.
Average_Pow = mean(abs(Tx).^2) % Compute the average power.
Tx = Tx/Scale; % Unscale
Rx = pamdemod(Tx,M); % Demodulate.
isequal(s,Rx)
Please revert, if facing problems in understanding the code.
If I am using the modulator/demodulator object in MATLAB does it normalize the output signal so that it has unit energy?
@shareef:
Yes, the equation 2/3*(M-1) can be used for QPSK (which an be considered as a simple 4-QAM).
Then the energy of constellation comes to 2. Hence the scaling factor is 1/sqrt(2).
~krishna
Hi, Krishna
The explanation for QAM and 16-QAM are very useful, what about QPSK isit the same as the above? if not how would be.
Thanks