When QAM (Quadrature Amplitude Modulation) is used, typically one may find a scaling factor associated with the constellation mapping operation. It may be reasonably obvious that this scaling factor is for normalizing the average energy to one. This post attempts to compute the average energy of the 16-QAM, 64-QAM and M-QAM constellation (where is a…
We had discussed three Single Input Multiple Output (SIMO also known as receive diversity) schemes – Selection combining, Equal Gain Combining, Maximal Ratio Combining and a Multiple Input Single Output (MISO, also known as transmit diversity) scheme – Alamouti 2×1 STBC. Let us now discuss the case where there a multiple transmit antennas and multiple…
In the previous post on transmit filtering using Nyquist pulse, we had briefly learned that the information symbol with a symbol period can be transmitted without inter symbol interference (ISI) by using Nyquist pulse, . The resultant waveform is ideally bandlimited to frequencies from Hz to Hz. However, in typical transmission schemes, we do not…
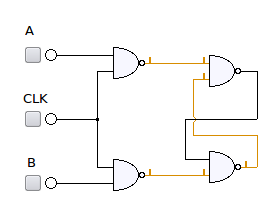
Question 6 on digital circuit from GATE (Graduate Aptitude Test in Engineering) 2012 Electronics and Communication Engineering paper. Q6. Consider the given circuit In this circuit, the race around (A) does not occur (B) occurs when CLK=0 (C) occurs when CLK=1 and A=B=1 (D) occurs when CLK=1 and A=B=0
Following a brief discussion with my friend Mr. Rethnakaran Pulikkoonattu on phase noise profiles, he pointed me to his write up on Oscillator Phase Noise and Sampling Clock Jitter . In this post, we will discuss the math behind integrating the phase noise power spectral density (in dBc/Hz) to find the root mean square jitter value.
This post discuss about the thermal noise in RC low pass filter. Using the noise equivalent model using resistor with a voltage source, which gets passed through a no noise RC low pass filter. The noise power at the output is computed by integrating the output voltage spectral density over all frequencies.
In DSP-Proakis, I found the problem 2.56 interesting as it provides insight into delta modulation. The task is to show that, where is any discrete time signal and is the unit step function.
Question 16 on electromagnetics from GATE (Graduate Aptitude Test in Engineering) 2012 Electronics and Communication Engineering paper. Q16. A coaxial cable with an inner diameter of 1mm and outer diameter of 2.4mm is filled with a dielectric of relative permittivity 10.89. Given , the characteristic impedance of the cable is (A) (B) (C) (D) Solution To…
Wishing all the readers of dsplog.com a great year 2010 ! Its been a mixed year for dsplog. Some key milestones a) Crossing 1000 subscribers with 1100+ comments in March 2009 b) Crossing 100 posts with 2200 subscribers and 2600+ comments in October 2009 c) As I write this, we have 102 posts with 2603…
Advanced Computing and Communication Society (ACS) of India is organizing ICCBN 2008 conference (International Conference on Communication, Convergence, and Broadband Networking) from July 17th to 20th 2008 at National Science Seminar Complex at Indian Institute of Science (IISc), Bangalore. ICCBN Conference aims to provide a premier forum for researchers, industry practitioners and educators to present…
Question 39 on communication from GATE (Graduate Aptitude Test in Engineering) 2012 Electronics and Communication Engineering paper. Q39. The signal as shown is applied both to a phase modulator (with as the phase constant) and a frequency modulator (with as the frequency constant) having the same carrier frequency. The ratio for the same maximum phase deviation is,…
In the previous post on Batch Gradient Descent and Stochastic Gradient Descent, we looked at two iterative methods for finding the parameter vector which minimizes the square of the error between the predicted value and the actual output for all values in the training set. A closed form solution for finding the parameter vector is possible, and in this post…
Question 15 on communication from GATE (Graduate Aptitude Test in Engineering) 2012 Electronics and Communication Engineering paper. Q15. A source alphabet consists of N symbols with the probability of the first two symbols being the same. A source encoder increases the probability of the first symbol by a small amount and decreases that of the…
In two previous posts, we have derived theoretical symbol error rate for 16-QAM and 16-PSK modulation schemes. The links are: (a) Symbol error rate for 16-PSK (b) Symbol error rate for 16-QAM Given that we are transmitting the same number of constellation points in both 16-PSK and 16-QAM, let us try to understand the better…