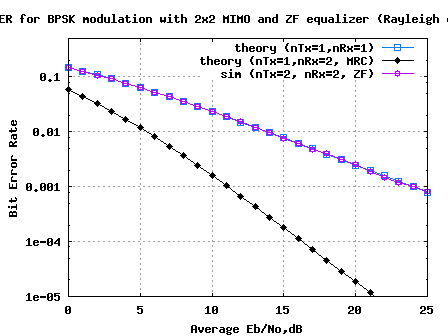
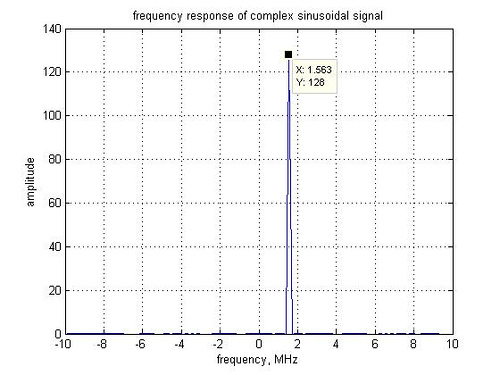
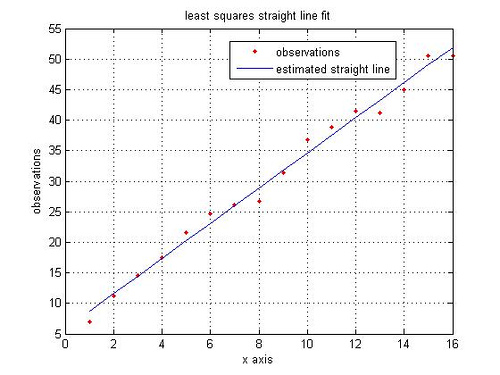
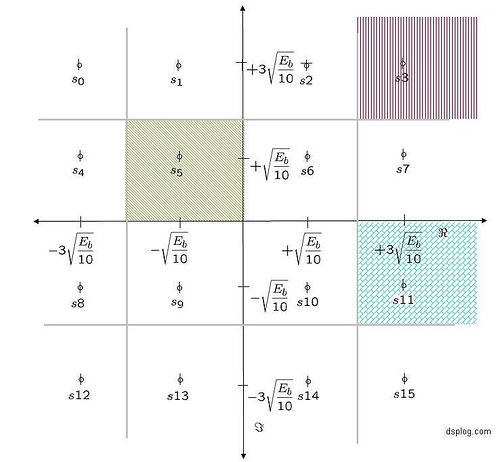
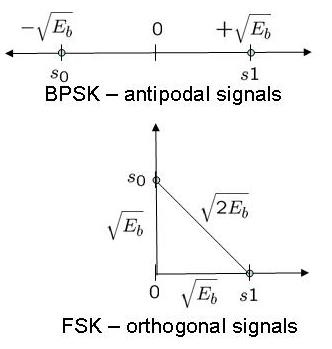
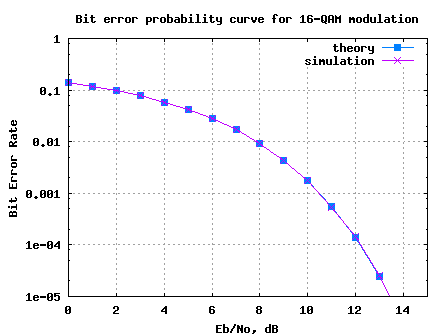
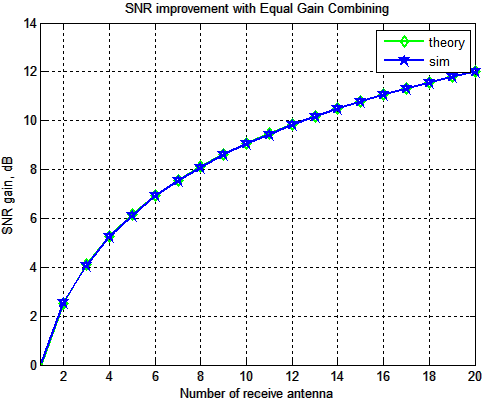
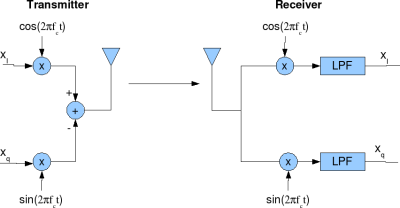
MCDES 2008 at Indian Institute of Science, Bangalore
Thanks to Prof. K V S Hari, I was informed that the centenary year for Indian Institute of Science (IISc), Bangalore starts on May 27th 2008. As part of the event, a conference with the theme Managing Complexity in a Distributed World (MCDES) is to be held at IISc from May27th to 31st 2008.