Loading ...
Question 52 on communication from GATE (Graduate Aptitude Test in Engineering) 2012 Electronics and Communication Engineering paper.
Q2. The power spectral density of a real process})
for positive frequencies is shown below. The values of \]})
and \]\|})
, respectively are
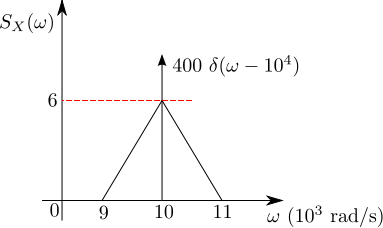
(A) 
(B) 
(C) })
(D) })
Solution
For a wide sense stationary function, the auto-correlation with delay is defined as,
From the Weiner-Kinchin theorem, the auto-correlation function and power spectral density
are Fourier Transform pairs, i.e.
Expressing in terms of , where
.
When the delay , the above equations simplifies to
.
Applying this to the problem at hand,
.
Further, since the power spectral density does not have any dc component, the mean of the signal
Based on the above, the right choice is (B)
References
[1] GATE Examination Question Papers [Previous Years] from Indian Institute of Technology, Madras http://gate.iitm.ac.in/gateqps/2012/ec.pdf
[3] Wide sense stationary function
[4] Auto-correlation
Related posts:
D id you like this article? Make sure that you do not miss a new article by subscribing to RSS feed OR subscribing to e-mail newsletter. Note: Subscribing via e-mail entitles you to download the free e-Book on BER of BPSK/QPSK/16QAM/16PSK in AWGN.
{ 0 comments… add one now }