Question 52 on electromagnetics from GATE (Graduate Aptitude Test in Engineering) 2012 Electronics and Communication Engineering paper.
An infinitely long uniform solid wire of radius  carries a uniform dc current of density
carries a uniform dc current of density  .
.
Q52. The magnetic field at a distance  from the center of the wire is proportional to
from the center of the wire is proportional to
(A)  for
for  and
and  for
for 
(B)  for
for  and
and  for
for 
(C)  for
for  and
and  for
for 
(D)  for
for  and
and  for
for 

Solution
To answer this question on magnetic field, we need to determine the magnetic field inside and outside the cable using Ampere’s Law.
Ampere’s Law :
The total current inside a closed curve
is the line integral of the magnetic field
(in Tesla)
,
where
is the magnetic field (in Tesla)
is the vector representing the infinitesimal line on the closed loop
,
is the net current enclosed by the closed loop and
is the permeability of vacuum.
Let us use this result to find the magnetic field in a uniform solid wire of radius .
Magnetic field in the region  :
:
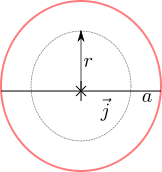
Figure : Solid wire showing the imaginary Amperian loop inside the wire (circle with radius )
Given that the current density is , the current through the area in the circle with radius
is
Applying Ampere’s law,
,
where
is the permeability (
is the permeability of vacuum.
is the permeability of the material).
Given that the magnetic field is is parallel to the line
and is uniform across the closed loop, it can be moved out of the integral, i.e
.
The term is the circumference of the circle with radius
i.e.
.
Substituting, the magnetic field in the region is,
.
Magnetic field in the region  :
:
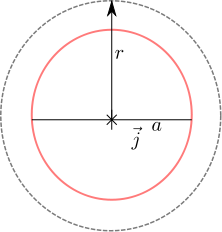
Figure : Solid wire showing the imaginary Amperian loop outside the wire (circle with radius )
Given that the current density is , the current through the area in the circle with radius
is determined only by the current flowing through the cable with in the radius
, i.e.
Applying Ampere’s law,
,
Taking outside the intergral and substituting for the term
,
The magnetic field in the region is,
.
Summarizing,
Based on the above, the right choice is (C) i.e. The magnetic field at a distance from the center of the wire is proportional to
for
and
for
References
[1] GATE Examination Question Papers [Previous Years] from Indian Institute of Technology, Madras http://gate.iitm.ac.in/gateqps/2012/ec.pdf
[2] Fields and Waves in Communication Electronics, Simon Ramo, John R. Whinnery, Theodore Van Duzer (buy from Amazon.com, buy from Flipkart.com).
[3] The youtube videos uploaded by user lasseviren1 aided me in understanding the integrals in electric field and magnetic field.
[4] Ampere’s Law
[5] Permeability