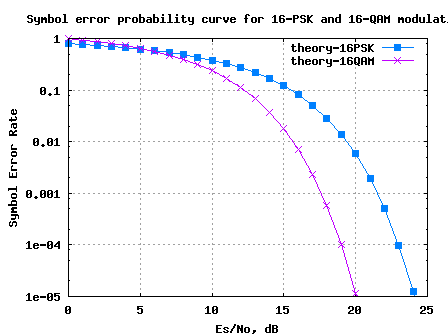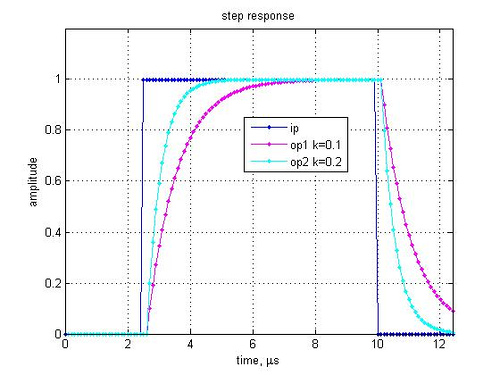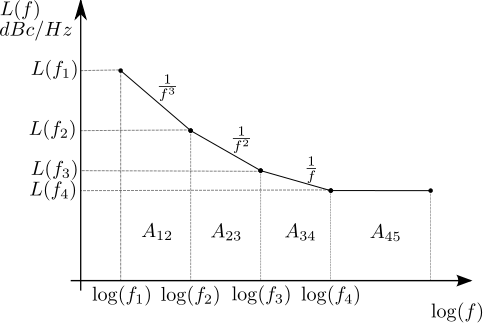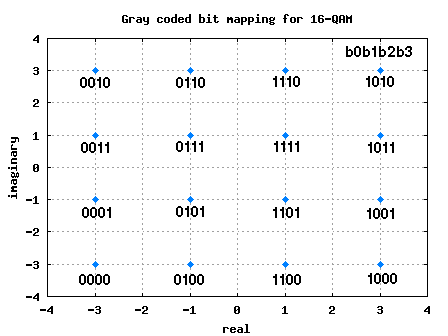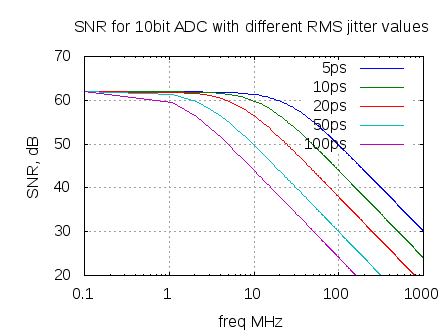
ADC SNR with clock jitter and quantization noise
My friend and colleague Mr. Vineet Srivastava pointed me to a nice article on clock jitter – Clock Jitter Effects on Sampling : A tutorial – by Carlos Azeredo-Leme, IEEE Circuits and Systems Magazine, Third Quarter 2011. In this post, let us discuss the total Signal to Noise Ratio at the output of an analog to…