Thanks to Prof. K V S Hari, I was informed that the centenary year for Indian Institute of Science (IISc), Bangalore starts on May 27th 2008. As part of the event, a conference with the theme Managing Complexity in a Distributed World (MCDES) is to be held at IISc from May27th to 31st 2008.
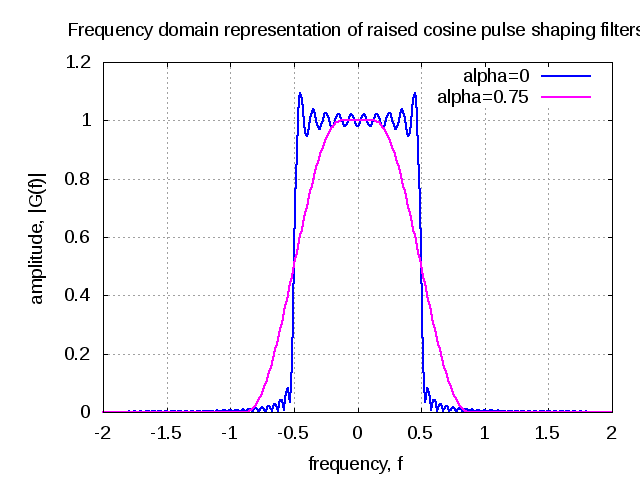
Question 3 on Communication from GATE (Graduate Aptitude Test in Engineering) 2012 Electronics and Communication Engineering paper. Q3. In a baseband communications link, frequencies upto 3500Hz are used for signalling. Using a raised cosine pulse with 75% excess bandwidth and for no inter-symbol interference, the maximum possible signaling rate in symbols per second is, (A)…
In two previous posts, we have discussed Convolutional Coding and the associated hard decision Viterbi decoding. In this post lets extent Viterbi decoding algorithm to soft input decision scheme. The modulation used is BPSK and the channel is assumed to be AWGN alone.
It might be interesting to interpret the output of the fft() function in Matlab. Consider the following simple examples. fsMHz = 20; % sampling frequency fcMHz = 1.5625; % signal frequency N = 128; % fft size % generating the time domain signal x1T = exp(j*2*pi*fcMHz*[0:N-1]/fsMHz); x1F = fft(x1T,N); % 128 pt FFT figure; plot([-N/2:N/2-1]*fsMHz/N,fftshift(abs(x1F)))…
In May 2008, we derived the theoretical symbol error rate for a general M-QAM modulation (in Embedded.com, DSPDesignLine.com and dsplog.com) under Additive White Gaussian Noise. While re-reading that post, felt that the article is nice and warrants a re-run, using OFDM as the underlying physical layer. This post discuss the derivation of symbol error rate for a general…
Question 12 on math from GATE (Graduate Aptitude Test in Engineering) 2012 Electronics and Communication Engineering paper. Q12. With initial condition the solution of the differential equation, is (A) (B) (C) (D) Solution From the product rule used to find the derivative of product of two or more functions, Applying this to the above equation, we…
Are you bothered by speed of the speed of the simulations which you develop in Matlab/Octave? I was not bothered much, till I ran into the Viterbi decoder. If you recall, the Matlab/Octave simulation script for BER computation with hard soft decision Viterbi algorithm provided in post Viterbi with finite survivor state memory took around…
Question 39 on communication from GATE (Graduate Aptitude Test in Engineering) 2012 Electronics and Communication Engineering paper. Q39. The signal as shown is applied both to a phase modulator (with as the phase constant) and a frequency modulator (with as the frequency constant) having the same carrier frequency. The ratio for the same maximum phase deviation is,…
In TETRA specifications, one of the modulation technique used is Differential 8 Phase Shift Keying (D8PSK). We will discuss the bit error rate with non-coherent demodulation of D8PSK in Additive White Gaussian Noise (AWGN) channel.
Question 15 on communication from GATE (Graduate Aptitude Test in Engineering) 2012 Electronics and Communication Engineering paper. Q15. A source alphabet consists of N symbols with the probability of the first two symbols being the same. A source encoder increases the probability of the first symbol by a small amount and decreases that of the…
This post discuss about the thermal noise in RC low pass filter. Using the noise equivalent model using resistor with a voltage source, which gets passed through a no noise RC low pass filter. The noise power at the output is computed by integrating the output voltage spectral density over all frequencies.
In an earlier post, it was mentioned that delta modulator without the quantizer is identical to convolving an input sequence with . Let us first try to validate that thought using a small MATLAB example and using the delta modulator circuit shown in Figure 9.13a of DSP-Proakis [1]. % delta modulation xn = sin(2*pi*1/64*[0:63]); xhatn…
In signal processing blocks like power estimation used in digital communication, it may be required to represent the estimate in log scale. This post explains a simple linear to log conversion scheme proposed in the DSP Guru column on DSP Trick: Quick-and-Dirty Logarithms. The scheme makes implementation of a linear to log conversion simple and…