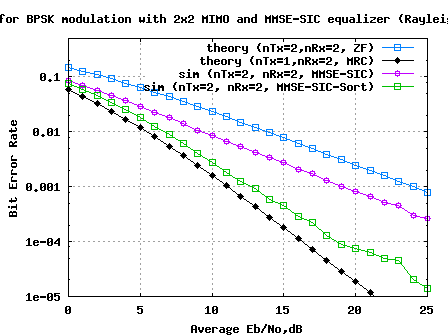
MIMO with MMSE SIC and optimal ordering
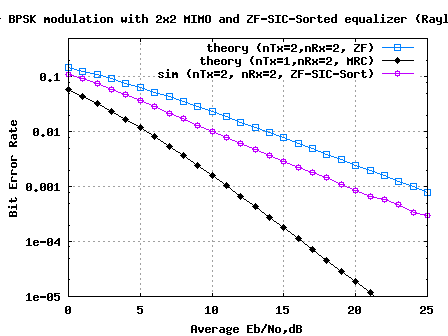
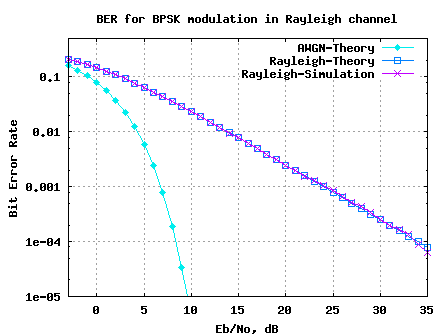
This post attempts to build further on the MIMO equalization schemes which we have discussed – (a) Minimum Mean Square Error (MMSE) equalization, (b) Zero Forcing equalization with Successive Interference Cancellation (ZF-SIC) and (c) ZF-SIC with optimal ordering. We have learned that successive interference cancellation with optimal ordering improves the performance with Zero Forcing equalization….