GATE-2012 ECE Q16 (electromagnetics)

Question 16 on electromagnetics from GATE (Graduate Aptitude Test in Engineering) 2012 Electronics and Communication Engineering paper.

Q16. A coaxial cable with an inner diameter of 1mm and outer diameter of 2.4mm is filled with a dielectric of relative permittivity 10.89. Given ${\mu_0=4\pi\mbox{x}10^{-7}\mbox{ H/m, }\epsilon_0={10^{-9}}/{36\pi}\mbox{ F/m}}$ , the characteristic impedance of the cable is

(A) ${330\mbox{\Omega}}$

(B) ${100\mbox{\Omega}}$

(C) ${143.3\mbox{\Omega}}$

(D) ${43.4\mbox{\Omega}}$

Solution

To answer this question, am referring to the discussion on capacitance per unit length (Section 1.9) , inductance per unit length (Section 2.4) and characteristic impedance (Section 5.2) of a coaxial cable from Fields and Waves in Communication Electronics, Simon Ramo, John R. Whinnery, Theodore Van Duzer (buy from Amazon.com, buy from Flipkart.com).

Finding the capacitance per unit length:

Using Gauss law :

For a closed Gaussian surface $S$ , the electrical flux is given by :

$\begin{array}\Phi_{\mbox{E}}&=&\oint_S{E}.{dA}&=&\frac{Q_s}{\Large{\epsilon_0}}\end{array}$ , where

$\begin{array}\Phi_{\mbox{E}}\end{array}$ is the electrical flux,

$E$ is the electric field,

$dA$ is the vector representing the infinitesimal area on the surface $S$ ,

$Q_s$ is the net charge enclosed by the surface and

$\epsilon_0$ is the permittivity of vacuum.

Let us use this result to find the electrical field in a coaxial cable formed by two conducting cylinders of radii $a$ and $b$ respectively with a dielectric $\epsilon$ between them (shown in the figure below).

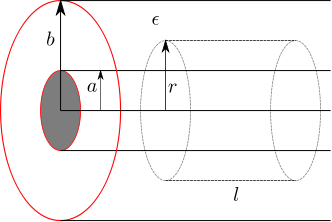
Figure : Coaxial cable showing the imaginary Gaussian surface (cylinder with radius $r$ and length $l$ )

For finding the electric field $E$ in region $\begin{array}a&<&r&<&b\end{array}$ , assume a cylindrical Gaussian surface of radius $r$ and length $l$ (as shown by the dashed line).

Applying Gauss law,

$\begin{array}\oint_S{E}.{dA}&=&\frac{Q_s}{\Large{\epsilon}}&=&\frac{q_ll}{\epsilon}\end{array}$ ,

where

$q_l$ is the charge per unit length,

total charge enclosed is the charge per unit length multiplied by the length i.e. $Q_s = q_ll$ and

$\epsilon=\epsilon_r \epsilon_0$ is the permittivity ( $\epsilon_0$ is the permittivity of vacuum, $\epsilon_r$ is the permittivity of the material).

Given that the electrical field is $E$ is parallel to the surface $dA$ and is uniform across the Gaussian surface, it can be moved out of the integral, i.e

$\begin{array}E\oint_S{dA}&=&\frac{q_ll}{\epsilon}\end{array}$ .

The term $\begin{array}\oint_S{dA}\end{array}$ is the surface area of the cylinder with radius $r$ of length $l$ and is,

$\begin{array}\oint_S{dA}&=&2\pi rl\end{array}$ .

Substituting, the electric field in the region $\begin{array}a&<&r&<&b\end{array}$ is,

$\begin{array}E&=&\frac{q_l}{2\pi\epsilon r}\end{array}$ .

With the above electric field, the potential difference between the coaxial cylinders is computed as,

$\begin{array}\phi_a - \phi_b &=&-\int_a^b\frac{q_ldr}{2\pi \epsilon r}\\&=&\frac{q_l}{2\pi\epsilon}\ln$\frac{b}{a}$\end{array}$ .

The capacitance between two electrodes is defined as the charge $Q$ on each electrode per volt of potential difference $\phi_a - \phi_b$ between then,

$C = \frac{Q}{\phi_a - \phi_b}$ .

Assuming that the field is only radial and the total charge per unit length is $q_l$ , the capacitance per unit length is

${\begin{array}C&=&\frac{2\pi\epsilon}{\ln$b/a$},&\mbox{ F/m}\end{aray}}$ .

Finding the inductance per unit length:

Using Ampere’s Law :

The total current $I_{enc}$ inside a closed curve $C$ is the line integral of the magnetic field $B$ (in Tesla)

$\begin{array}\oint_C{B}.{dl}&=&\mu_oI_{enc}\end{array}$ ,

where

$B$ is the magnetic field (in Tesla)

$dl$ is the vector representing the infinitesimal line on the closed loop $C$ ,

$I_{enc}$ is the net current enclosed by the closed loop and

$\mu_0$ is the permeability of vacuum.

Let us use this result to find the magnetic field in a coaxial cable formed by two conducting cylinders of radii $a$ and $b$ respectively with a dielectric having permeability of $\mu$ between them (shown in the figure below).

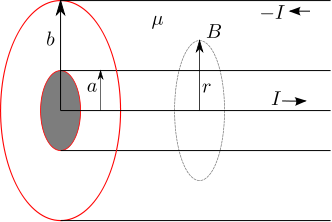
Figure : Coaxial cable showing the imaginary Amperian loop (circle with radius $r$ )

Applying Ampere’s law,

$\begin{array}\oint_C{B}.{dl}&=&\mu I\end{array}$ ,

where

$\mu=\mu_r \mu_0$ is the permeability ( $\mu_0$ is the permeability of vacuum. $\mu_r$ is the permeability of the material).

Given that the magnetic field is $B$ is parallel to the line $dl$ and is uniform across the closed loop, it can be moved out of the integral, i.e

$\begin{array}B\oint_C{dl}&=&\mu I\end{array}$ .

The term $\begin{array}\oint_C{dl}\end{array}$ is the circumference of the circle with radius $r$ and is, $\begin{array}\oint_C{dl}&=&2\pi r\end{array}$ .

Substituting, the magnetic field in the region $\begin{array}a&<&r&<&b\end{array}$ is,

${\begin{array}B&=&\frac{\mu I}{2\pi r}\end{array}}$ .

The inductance is defined as ratio of magnetic field over a surface and the the current.

$\begin{array}L&=&\frac{1}{I}\int_SB.dS\end{array}$ .

For a unit length, the integral of magnetic field in the region $\begin{array}a&<&r&<&b\end{array}$ is,

$\begin{array}\int_SB.dS&=&\int_a^b\mu\frac{I}{2\pi r}dr&=&\frac{\mu I}{2\pi}\ln\(b/a)\end{array}$ .

Substituting, the inductance per unit length is,

$\begin{array}L&=&\frac{\mu}{2\pi}\ln$b/a$&\mbox{ H/m}\end{array}$ .

Note :

YouTube videos uploaded by user lasseviren1 aided me in understanding the integrals in electric field and magnetic field. Do checkout the play-lists : Gauss’s Law , Sources of Magnetic Fields

The characteristic impedance :

From wiki entry on characteristic impedance, the general expression for the characteristic impedance of a transmission line is

$\begin{array}Z_0&=\sqrt{\frac{R+j\omega L}{G+j\omega C}}\end{array}$ ,

where,

$R$ is the resistance per unit length,

$L$ is the inductance per unit length,

$C$ is the capacitance per unit length,

$G$ is the conductance per unit length and

$\omega$ is the angular frequency.

Assuming a loss less transmission line, i.e. $R=G=0$ , the equation reduces to,

$\begin{array}Z_0&=\sqrt{\frac{L}{C}}\end{array}$ .

Substituting the expressions for inductance per unit length and capacitance per unit length for a coaxial cable,

${\begin{array}Z_0&=\sqrt{\frac{\mu}{\epsilon}}\frac{\ln$b/a$}{2\pi}\end{array}}$ .

Substituting the numbers from the problem at hand,

$\mu \simeq \mu_0 = 4\pi\mbox{x}10^{-7}$

$\epsilon =\epsilon_0 \epsilon_r = 10^{-9}/{36\pi} * 10.89$

$b = 2.4$

$a = 1$ ,

the characteristic impedance is,

$\begin{array}Z_0&=&15.918\end{array}$ .

The calculated choice is not listed in the options. However if we ignore the $\2\pi$ term, the calculated number comes to around $100$ . That does not help, does it? 🙂

References

[1] GATE Examination Question Papers [Previous Years] from Indian Institute of Technology, Madras http://gate.iitm.ac.in/gateqps/2012/ec.pdf

[2] Fields and Waves in Communication Electronics, Simon Ramo, John R. Whinnery, Theodore Van Duzer (buy from Amazon.com, buy from Flipkart.com).

[3] The youtube videos uploaded by user lasseviren1 aided me in understanding the integrals in electric field and magnetic field. Do checkout the play-lists : Gauss’s Law

Sources of Magnetic Fields

[4] Characteristic impedance

[5] Ampere’s Law

[6] Gauss law

[7] Permeability

[8] Permittivity

[9] Electrical Flux

Migrated to Amazon EC2 instance (from shared hosting)

GATE-2012 ECE Q28 (electromagnetics)

Image Rejection Ratio (IMRR) with transmit IQ gain/phase imbalance

GATE-2012 ECE Q15 (communication)

GATE-2012 ECE Q7 (digital)

GATE-2012 ECE Q13 (circuits)

GATE-2012 ECE Q16 (electromagnetics)

Q16. A coaxial cable with an inner diameter of 1mm and outer diameter of 2.4mm is filled with a dielectric of relative permittivity 10.89. Given ${\mu_0=4\pi\mbox{x}10^{-7}\mbox{ H/m, }\epsilon_0={10^{-9}}/{36\pi}\mbox{ F/m}}$ , the characteristic impedance of the cable is

(A) ${330\mbox{\Omega}}$

(B) ${100\mbox{\Omega}}$

(C) ${143.3\mbox{\Omega}}$

(D) ${43.4\mbox{\Omega}}$

Solution

Finding the capacitance per unit length:

Finding the inductance per unit length:

The characteristic impedance :

References

Leave a Reply Cancel reply

Q16. A coaxial cable with an inner diameter of 1mm and outer diameter of 2.4mm is filled with a dielectric of relative permittivity 10.89. Given , the characteristic impedance of the cable is

(A)

(B)

(C)

(D)

Solution

Finding the capacitance per unit length:

Finding the inductance per unit length:

The characteristic impedance :

References

Leave a Reply Cancel reply

Related Articles

Q16. A coaxial cable with an inner diameter of 1mm and outer diameter of 2.4mm is filled with a dielectric of relative permittivity 10.89. Given ${\mu_0=4\pi\mbox{x}10^{-7}\mbox{ H/m, }\epsilon_0={10^{-9}}/{36\pi}\mbox{ F/m}}$ , the characteristic impedance of the cable is

(A) ${330\mbox{\Omega}}$

(B) ${100\mbox{\Omega}}$

(C) ${143.3\mbox{\Omega}}$

(D) ${43.4\mbox{\Omega}}$