In the post on Soft Input Viterbi decoder, we had discussed BPSK modulation with convolutional coding and soft input Viterbi decoding in AWGN channel. Let us know discuss the derivation of soft bits for 16QAM modulation scheme with Gray coded bit mapping. The channel is assumed to be AWGN alone.
Gray Mapped 16-QAM constellation
In the past, we had discussed BER for 16QAM in AWGN modulation. The 4 bits in each constellation point can be considered as two bits each on independent 4-PAM modulation on I-axis and Q-axis respectively.
| b0b1 | I | b2b3 | Q |
| 00 | -3 | 00 | -3 |
| 01 | -1 | 01 | -1 |
| 11 | +1 | 11 | +1 |
| 10 | +3 | 10 | +3 |
Table: Gray coded constellation mapping for 16-QAM
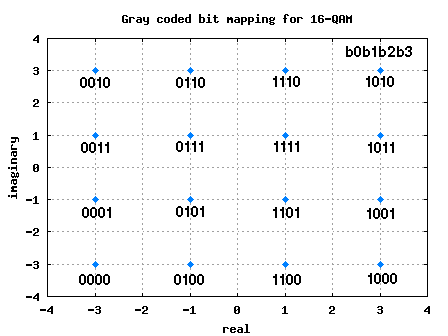
Figure: 16QAM constellation plot with Gray coded mapping
Channel Model
The received coded sequence is
, where
is the modulated coded sequence taking values in the alphabet
.
is the Additive White Gaussian Noise following the probability distribution function,
with mean
and variance
.
Demodulation
For demodulation, we would want to maximize the probability that the bit was transmitted given we received
i.e
. This criterion is called Maximum a posteriori probability (MAP).
Using Bayes rule,
.
Note: The probability that all constellation points occur are equally likely, so maximizing is equivalent to maximizing
.
Soft bit for b0
The bit mapping for the bit b0 with 16QAM Gray coded mapping is shown below. We can see that when b0 toggles from 0 to 1, only the real part of the constellation is affected.
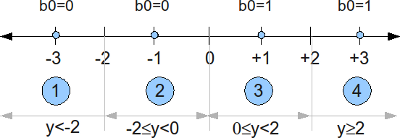
Figure: Bit b0 for 16QAM Gray coded mapping
When the b0 is 0, the real part of the QAM constellation takes values -3 or -1. The conditional probability of the received signal given b0 is 0 is,
.
When the bit0 is 1, the real part of the QAM constellation takes values +1 or +3. The conditional probability given b0 is zero is,
.
We can define a likelihood ratio that if
.
The likelihood ratio for b0 is,
.
Region #1 ( )
)
When , then we can assume that relative contribution by constellation +3 in the numerator and -1 in the denominator is less and can be ignored. So the likelihood ratio reduces to,
.
Taking logarithm on both sides,
.
Region #2 ( ), Region #3 (
), Region #3 ( )
)
When or
, then we can assume that relative contribution by constellation +3 in the numerator and -3 in the denominator is less and can be ignored. So the likelihood ratio reduces to,
.
Taking logarithm on both sides,
.
Region #4 ( )
)
If , then we can assume that relative contribution by constellation +1 in the numerator and -3 in the denominator is less and can be ignored. So the likelihood ratio reduces to,
.
Taking logarithm on both sides,
.
Soft bit for b1
The bit mapping for the bit b1 with 16QAM Gray coded mapping is shown below. We can see that when b0 toggles from 0 to 1, only the real part of the constellation is affected.
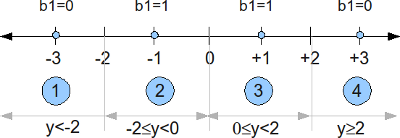
Figure: Bit b1 for 16QAM Gray coded mapping
When the b1 is zero, the real part of the QAM constellation takes values -3 or +3. The conditional probability given b1 is zero is,
.
When the bit0 is 1, the real part of the QAM constellation takes values -1 or +1. The conditional probability given b1 is one is,
.
We can define a likelihood ratio that if
.
The likelihood ratio for b1 is,
.
Region #1 ( ), Region#2 (
), Region#2 ( )
)
When or
, then we can assume that relative contribution by constellation +1 in the numerator and +3 in the denominator is less and can be ignored. So the likelihood ratio reduces to,
.
Taking logarithm on both sides,
.
Region #3 ( ), Region #4 (
), Region #4 ( )
)
If or
, then we can assume that relative contribution by constellation -1 in the numerator and -3 in the denominator is less and can be ignored. So the likelihood ratio reduces to,
.
Taking logarithm on both sides,
.
Summary
Note: As the factor is common to all the terms, it can be removed.
The softbit for bit b0 is,
.
The softbit for bit b1 is,
.
The softbit for bit b1 can be simplified to,
.
It is easy to observe that the softbits for bits b2, b3 are identical to softbits for b0, b1 respectively except that the decisions are based on the imaginary component of the received vector .
The softbit for bit b2 is,
.
The softbit for bit b3 is,
.
As described in the paper, Simplified Soft-Output Demapper for Binary Interleaved COFDM with Application to HIPERLAN/2, Filippo Tosato1, Paola Bisaglia, HPL-2001-246 October 10th , 2001, the term
and
,
This simplification avoids the need for having a threshold check in the receiver for sofbits b0 and b2 respectively.
Hello Krishna,
Can you please advise if you have some information on the soft output de-mapping for 8PSK?
Thanks
Yogesh
@Yogesh: I have not written on that topic
Thanks a lot, it has a good flow, easily understandable and was really useful 🙂
Nice article, very clear and easy to understand. Thanks a lot !
@Chandima: Glad to be of help.
Hello Krishna
Great job with the article!!.
I have the following question. How these calculations are linked to the use of turbo decoding, I think that the input to turbo decoding are these values (LLRs -Softbits), is that correct? Thank you very much!
Felipe
@Felipe: Hmm… typically any decoder which can take soft information can use this. I had Viterbi decoder in my mind when writing this post.
Hi Krishna,
In the section “Soft bit for b1”, there are several typos.
Like “The conditonal prbability given b0 is zero is,”. It should be b1, right? In the following discription, there are several b0 emerge, but I think all should be b1.
@Xia: Thanks much again. It is a copy-paste error – and I spotted couple more around what you described. Corrected all those. Sorry for the typos.
Hi Krishna,
In your discription, it says b0 = 1, if P(y|b0 = 1) / P(y|b0 = 0) >= 0.
But I think the likelihood ratio test should be compared with 1 instead of 0.
Like this P(y|b0 = 1) / P(y|b0 = 0) >= 1.
There is no log in front of the ratio.
@Xia: Thanks much for pointing that out. I corrected it.
Hi Krishna,
please clarify a doubt of mine
1.In hard decision viterbi decoder, we use hamming distance as criterion..meaning. we get the hard decided points and compute the distance between hard decided points and EXPECTED points in that branch
2. In soft decision, we use euclidean distance..meaning..whatever received constellation point we get, we take them forward and compute the distance between received constellation point and EXPECTED constellation points in that branch
3. can you please tell me where is this LLR fitting into this whole scenario.
Thanks
aizza ahmed
@aizza: The LLR (log likelihood ratio) captures the likelihood of the received symbol corresponding to transmission of bit zero OR one. The log likelihood ratio is used to compute the euclidean distance.
Helps?
http://www.scribd.com/doc/24329042/Hindawi-Publishing-Corporation-Research-Letters-in-Communications-Volume-2007-Article
This article is also more near to your article..what your wrote..
Thank you again Mr. Krishna.
Btw, when I copy the above page, some equations could not be copied. I like to copy in Win Word and print it. I use to study by paper and make notes in the paper.
Regards,
@andjas: For each article, there is “Print” option in the top right corner. Did you try using that? Maybe that helps.
aaaahh,
thank you Krishna.
Btw, I think there are some mistype.
It type ‘r’ rather than ‘y_er’.
in last equation of:
– soft bit b0, region 3
– soft bit b1, region 1&2
@andjas: I was unable to find the typo. Can you please point that out.
IMHO,
Btw, I think there are some mistype.
It type ‘r’ rather than ‘y_er’.
in last equation of:
– soft bit b0, region 3
– soft bit b1, region 1&2
This is the snapshot of it.
http://andjaswahyu.files.wordpress.com/2010/11/16qam_llr_mistype.png
@andjas: corrected the typo. thanks for pointing that out
Hi,
I am working on a QAM-16 modem,
can you help me please to implement it on MTLAB
regards
@Mohamed Hedi: You can look at articles @ https://dsplog.com/tag/qam
Hopefully, it helps.
hello krishna
I have a question, as for the softbit for 16-QAM, if the channel is not AWGN but exponentical decay , how can I get the softbit?
Thanks,
xiaonaren
@xiaonaren: Am not sure of the case where there is ISI. However, if its only flat fading, the above equations with additional scaling factor for channel gain should hold good
hello krishna
i have a question , why two and four phase psk have same figure in plotting of SNR (per bit)(horizontal axis) in term Pb (probability of error)(vertical axis)? in page 225 of digital communication proakis 5ed
any good reference for complete explanation
@sam: Well with 4-PSK, the modulation is performed on two orthogonal dimensions. Hence the noise added on one dimension will not affect the other. Hence the BER is the same.
thanks,it’s a clear,simple computing of LLR.
@ruoyu: Glad 🙂
Hey Krishna,
Along the line of soft decoding, do you plan to write some articles on chase combining?
Thanks,
Zhongren
@Zhongren: I have not yet tried modeling any automatic repeat request (ARQ) schemes and correspondingly chase combining. I will add to my to-do list.
Hi Krishna!
I hope you are doing great. I have a very basic question. I am implementing OFDM system in matlab. r_k are my received symbols and s_k are my transmitted symbols, where k is the subcarrier index. Now at the receiver, after zero forcing equalizer, I want to find the variance i.e. var = E[|r_k – s_k|²], but I dont know how to implement this equation in matlab… kindly help
best regards,
invizi.
@invizible: Thanks, am doing good. Hope you are fine too.
Well, in Matlab mean(abs(r_k – s_k).^2) should do the job for you.
Thanks alot … you are doing a very fine job … Krishna the great
clearly.
thx a lot.