Equivalence of Moving Average and CIC filter
Let me briefly share my understanding on the cascaded integrator comb (CIC) filter, thanks to the nice article. For understanding the cascaded integrator comb (CIC) filter, firstly let us understand the moving average filter, which is accumulation latest samples of an input sequence
.
Figure: Moving average filter
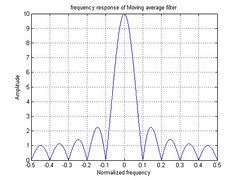
The frequency response of the moving average filter is:
.
% Moving Average filter
N = 10;
xn = sin(2*pi*[0:.1:10]);
hn = ones(1,N);
y1n = conv(xn,hn);
% transfer function of Moving Average filter
hF = fft(hn,1024);
plot([-512:511]/1024, abs(fftshift(hF)));
xlabel(‘Normalized frequency’)
ylabel(‘Amplitude’)
title(‘frequency response of Moving average filter’)
Figure: Frequency response of moving average filter
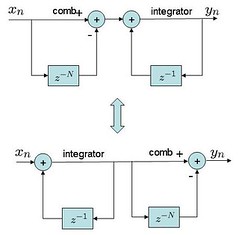
The moving average filter which is implemented as a direct form FIR type as shown above can also be implemented in a recursive form. It consists of a comb stage whose output is difference of the current sample and the sample which cameprior. The difference is successively accumulated by an integrator stage. Together the circuits behave identically as the moving average filter described prior.
It can be proved using a simple proof that:
Figure: Cascaded Integrator Comb Filter
Bit more details can be found in Sec2.5.2 Recursive and Non Recursive Realization of FIR systems in [DSP-PROAKIS].
As the system is linear, the position of the integrator and comb stage can be swapped. Now, using a small Matlab code snippet let us verify that the output from CIC realization is indeed the same as obtained from moving average filter.
% Implementing Cascaded Integrator Comb filter with the
% comb section following the integrator stage
N = 10;
delayBuffer = zeros(1,N);
intOut = 0;
xn = sin(2*pi*[0:.1:10]);
for ii = 1:length(xn)
% comb section
combOut = xn(ii) – delayBuffer(end);
delayBuffer(2:end) = delayBuffer(1:end-1);
delayBuffer(1) = xn(ii);
% integrator
intOut = intOut + combOut;
y2n(ii) = intOut;
end
err12 = y1n(1:length(xn)) – y2n;
err12dB = 10*log10(err12*err12’/length(err12)) % identical outputs
close all
% Implementing Cascaded Integrator Comb filter with the
% integrator section following the comb stage
N = 10;
delayBuffer = zeros(1,N);
intOut = 0;
xn = sin(2*pi*[0:.1:10]);
for ii = 1:length(xn)
% integrator
intOut = intOut + xn(ii);
% comb section
combOut = intOut – delayBuffer(end);
delayBuffer(2:end) = delayBuffer(1:end-1);
delayBuffer(1) = intOut;
y3n(ii) = combOut;
end
err13 = y1n(1:length(xn)) – y3n;
err13dB = 10*log10(err13*err13’/length(err13)) % identical outputs
The outputs are matching.
The recursive realization of the FIR filter as described above helps to achieve the same result with less hardware.
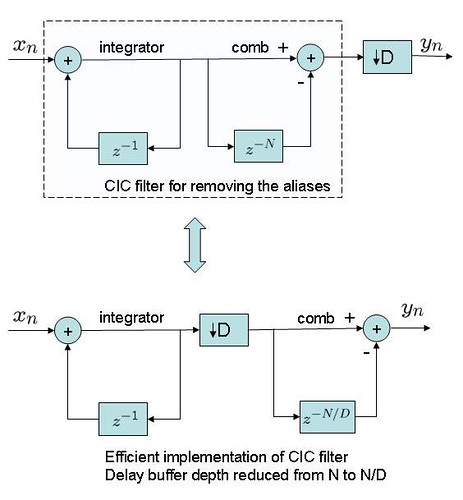
Using CIC filter for decimation
Typically, decimation to a lower sampling rate is achieved by taking one sample out of every samples. There exists an anti-aliasing filter to remove the un-desired spectrum before decimation.
Figure: CIC filters for decimation
As shown above, the same output can be achieved by having the decimation stage between integrator stage and comb stage. This helps in reducing the delay buffer depth requirement of the comb section. Using a small Matlab code snippet, let us check whether both the implementations behave identically.
% For decimation, having the CIC filtering before taking every other sample
D = 2; % decimation factor
N = 10; % delay buffer depth
delayBuffer = zeros(1,N); % init
intOut = 0;
xn = sin(2*pi*[0:.1:10]);
y6n = [];
for ii = 1:length(xn)
% comb section
combOut = xn(ii) – delayBuffer(end);
delayBuffer(2:end) = delayBuffer(1:end-1);
delayBuffer(1) = xn(ii);
% integrator
intOut = intOut + combOut;
y6n = [y6n intOut];
end
y6n = y6n(1:D:end); % taking every other sample – decimation
% For efficient hardware implementation of the CIC filter, having the
% integrator section first, decimate, then the comb stage
% Gain : Reduced the delay buffer depth of comb section from N to N/D
D = 2; % decimation factor
N = 10; % delay buffer depth
delayBuffer = zeros(1,N/D);
intOut = 0;
xn = sin(2*pi*[0:.1:10]); % input
y7n = []; % output
for ii = 1:length(xn)
% integrator
intOut = intOut + xn(ii);
if mod(ii,2)==1
% comb section
combOut = intOut – delayBuffer(end);
delayBuffer(2:end) = delayBuffer(1:end-1);
delayBuffer(1) = intOut;
y7n = [ y7n combOut];
end
end
err67 = y6n – y7n;
err67dB = 10*log10(err67*err67’/length(err67))
The outputs are matching.
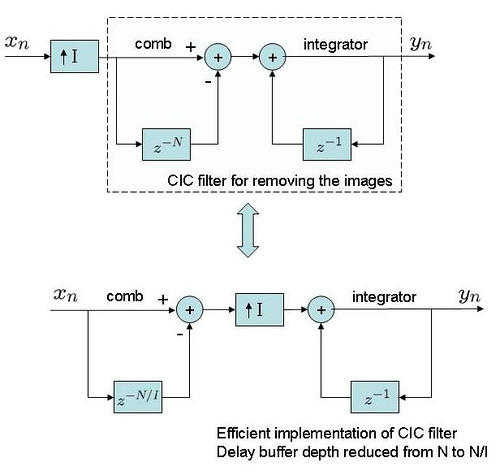
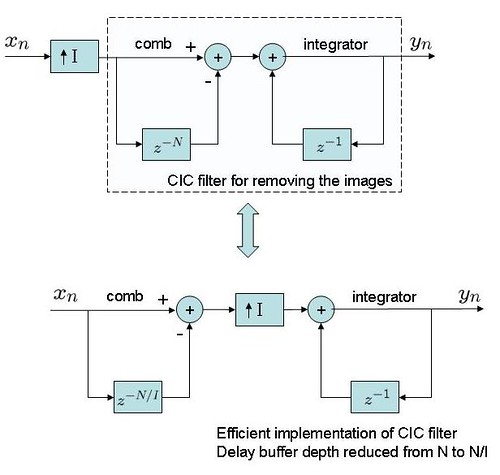
Using CIC filters for interpolation
Typically, interpolation to a higher sampling rate achieved by inserting zeros between consecutive samples followed by filtering (for removing the images).
Figure: Using CIC filters for interpolation
As shown above, the same result can be achieved by having the upsampling stage between comb and integrator stage. This helps in reducing the delay buffer depth requirement of the comb section. Using a small Matlab code snippet, let us check whether both the implementations behave identically.
% For interpolation, insert the zeros followed by CIC filtering
xn = sin(2*pi*[0:.1:10]);
I = 2; % interpolation factor
N = 10; % filter buffer depth
xUn = [xn; zeros(1,length(xn))];
xUn = xUn(:).’; % zeros inserted
delayBuffer = zeros(1,N);
intOut = 0;
for ii = 1:length(xUn)
% comb section
combOut = xUn(ii) – delayBuffer(end);
delayBuffer(2:end) = delayBuffer(1:end-1);
delayBuffer(1) = xUn(ii);
% integrator
intOut = intOut + combOut;
y4n(ii) = intOut;
end
% For efficient hardware implementation of CIC filter for interpolation, having
% the comb section, then zeros insertion, followed by integrator section
% Gain : Reduced the delay buffer depth of comb section from N to N/I
I = 2; % interpolation factor
N = 10; % original delay buffer depth
delayBuffer = zeros(1,N/I); % new delay buffer of N/I
intOut = 0;
xn = sin(2*pi*[0:.1:10]);
y5n = [];
for ii = 1:length(xn)
% comb section
combOut = xn(ii) – delayBuffer(end);
delayBuffer(2:end) = delayBuffer(1:end-1);
delayBuffer(1) = xn(ii);
% upsampling
combOutU = [ combOut zeros(1,1)];
for jj =0:I-1
% integrator
intOut = intOut + combOutU(jj+1);
y5n = [y5n intOut];
end
end
err45 = y4n – y5n;
err45dB = 10*log10(err45*err45’/length(err45)) % outputs matching
The outputs are matching.
One one question: Upsampling by a factor which is achieved by repeating the sample
times result in the same output as obtained by the CIC filter implementation described above (see previous post trying to describe that zero-order hold for interpolation). Considering so, do we need to have the filtering hardware when doing interpolation? I do not think so. If I have some additional thoughts, I will update.
References:
[1] Understanding cascaded integrator-comb filters – By Richard Lyons, Courtesy of Embedded Systems Programming URL: http://www.us.design-reuse.com/articles/article10028.html
[2] Digital Signal Processing – Principles, Algorithms and Applications, John G. Proakis, Dimitris G. Manolakis


thank you very much for your explanation.
Now i understood completely about CIC filter and its advantage.
delay buffer depth??
How do you decide ‘delay buffer depth’??
@Hyeukjin,Lim: Based on the filter cut off bandwidth required. Larger delay buffer depth translates to a lower cut off …
Dear All,
I would like to know if there is some one who can show me an Matlab example which performs the Comb Filter Logic which is explained here in the below links. Any one logic will be enough to start with. This will help me to go forward with the filter implementation. It is very urgent for me as I have to meet my deadlines.
https://www.dropbox.com/s/5nhmxqgveytl0ba/Comb%20FIR%20Filter%20Explanation.jpg
(or)
https://www.dropbox.com/s/5nhmxqgveytl0ba/Comb%20FIR%20Filter%20Explanation.jpg
thanking you in advance for understanding!
Prashant
Dear Krishna,
I want to know if I want to share files in this site then how can I do that? For example when I have a problem in MATLAB coding and I want to share file to show the people how I am coding it, as some times the codes are too long to paste here then it makes simpler to share the files instead.
Greetings
@Prashant: Well, you can upload to a public place like dropbox (or something equivalent) and share the link
Dear Krishna,
Here I have a FIR Comb Filter *.m file but I don’t know how I can modify it to meet my requirements as explained in my previous posts.
https://dl.dropbox.com/u/91710211/Comb%20Filter%20m%20Files/comb.m
https://dl.dropbox.com/u/91710211/Comb%20Filter%20m%20Files/TS.m
You need to just run TS.m file and you will see output of a Comb filter. I don’t if that will be helpful to both of my questions.
Greetings
Prashant
@Prashant: Knowing the sampling frequency of your systems, one can find where the nulls of the comb are present.
Hallo Krishna,
I would like to know if there is a possibility to speak to you about my issue? If that is possible then it will be very helpful as I am getting close to my deadlines. Kindly let me know by what means will it be possible?
Sincerely
Prashant
@Prashant: Please look at my previous replies. Hope that helps
Dear Krishna,
Apart from my previous post I have also the same Issue with a different requirement. Below are the link which shows what I am looking for. But the problem is how do I implement that? Here in this case I want to see only odd harmonics only in the output transfer function. I have never worked with ‘Comb Type FIR Filters’ so I am lost here.
I will be very grateful to you if you have a solution for such problem.
http://img821.imageshack.us/img821/7016/combfifofirfilter.jpg
The Below link shows how the buffer length ‘K’, Delay element Z^-1 & transmitted frequencies (Transfer Function) vary.
http://img826.imageshack.us/img826/4497/combfifofirfiltertabel.jpg
It will be very helpful in my project if you have any solution for such problem.
Thanking you!
Sincerely
Prashant.S
@Prashant: To get a comb response, one can use a circuit having a response as
y[n] = x[n] – x[n-D], where D is the delay
Putting D = 16, we can get a frequency response as follows:
B = [1 zeros(1,15) -1];
A = 1;
H W] = freqz([1 zeros(1,15) -1], [1],1024,’twosided’);
plot([-512:511]/1024,10*log10(abs(fftshift(H))));
Hope this helps.
Hi krishna,
So I think ‘D’ will be order of the filter, right?
How can I mention the sampling freqency ‘Fs’ of this filter?
If your code is for this: https://www.dropbox.com/s/5nhmxqgveytl0ba/Comb%20FIR%20Filter%20Explanation.jpg
What part of this code tells me the following:
If Fs=1KHz, Input signal Period=1 then,
Buffer Length= (Input signal period/2)* Fs = (1/2)*Fs=500
There for:
First sample coming out of the Buffer=Buffer Length/Fs=500/1KHz=0.5 sec
Kindly guide me How I can determine these from the filter code.
Sincerely
Prashant
@Prashant: The concept of sampling frequency is notional in matlab. If we assume that sampling frequency is fs=1kHz, for the example with D=16, the nulls of the comb filter lies at +/-125Hz, +/-250Hz, +/-375Hz
B = [1 zeros(1,15) -1];A=1;
[H W] = freqz(B,A,1024,’twosided’);
plot([-512:511]/1024*1000,10*log10(abs(fftshift(H))));
xlabel(‘freq, Hz’);ylabel(‘amplitude, dB’);grid on
octave:22> axis([-500 500 -15 5])
i want to plot the magnitude response of CIC filter.Thanks in advance.That would help me a lot.
@liguo: You can plot the frequency response of the moving average filter as
% Moving Average filter
N = 10;
xn = sin(2*pi*[0:.1:10]);
hn = ones(1,N);
y1n = conv(xn,hn);
% transfer function of Moving Average filter
hF = fft(hn,1024);
plot([-512:511]/1024, abs(fftshift(hF)));
xlabel(‘Normalized frequency’)
ylabel(‘Amplitude’)
title(‘frequency response of Moving average filter’)
sir i need exact defination of cic filter……need of cic flter ,working ,advantages and disadvantages of cic filter……………..please send it as soon as possible
@arunraj: does this post help?
i want to plot the magnitude response of comb filter…..anyone help me with Matlab code…Thanks in advance………cic fiter 🙂
@Bhavani: Hope this matlab code snippet helps.
% freq response
h_comb = [1 zeros(1,7) -1];
hF = fft(h_comb,1024);
plot([-512:511]/1024, 10*log10(abs(fftshift(hF))))
xlabel(‘normalized frequency’); ylabel(‘amplitude, dB’); title(‘Amplitude response of comb filter’);
grid on;
I’m very interested about the next:
You said:
“Considering so, do we need to have the filtering hardware when doing interpolation? I do not think so. ”
Is there a way to replace the block “arrow up, I”,with zero-hold block(which passes the value of the input signal to the output instead of inserting a zero between samples).
How i can realize that in matlab?
@Alexander: You can insert zeros and then convolve with a rectangular window
For eg,
xt = [1 zeros(1,2) 2 zeros(1,2) 3 zeros(1,2)];
ht = ones(1,3);
yt = conv(xt,ht);
hello krishna
nice to see your article on cic decimation filter
i am having problem with frequency response of cic specifically i want to improve it
can you help me i will be highly obiliged
@richa: Please provide more details of the problem which you are facing.
hello..
We are doing our project on uwb signal in nano seconds ..we need code for down sampling that received wideband signal after bandpass filtering.plz help us sir
@jennifer: Sorry, I have not tried modeling UWB signals. However,
for downsampling by factor of 2, take one sample every two samples;
for downsampling by factor of 3, take one sample every three samples; and so on
hi. i had a homework to do but i can’t do it. so please i need your help to solve it. it’s about matlab and digital signal processing.
@mike_cv: What is the help which you are looking for
Hi Krishna,
I still can not understand whether we must use digital low pass filter after interpolation. In fact , for upsampling, there is no aliasing issue at all and also the spectrum of the interpolation sequence is still periodic through low pass filter. To my understanding, after interpolation without low pass filter we can deliver the signal to DAC module directly to get the analog signal in time domain.Right ?
In addition, is there any other way to understand whether we can move the Decimation from the end of the cic to the mid of the cic without the help of matlab? That is to say, could we understand this by formula?
@thomas: My replies:
1/ Any digital signal will have spectrum from -infinity to +infinity. So, if we do not use the low pass filter, we will be transmitting the original spectrum plus all the replicas. And this is not desirable.
Yes, one can drive the output of the interpolation (inserting of zeros between samples) and pass to the DAC. However, note that most DAC’s have a zero-order hold transfer function i.e. hold on to the previous sample till the next sample has arrived. This zero-order hold is simple rectangular filter with sinc shaped frequency response.
2/ I have not tried playing with the math. However, it seems that once we write the transfer function of each stage, we should be able to get the equivalence.
Hi!
One question. If I have to create harmonics of a audio signal… I want make a basic integrator, that it have harmonic distorsion. Can you help?
I want a filter coefficients (A and B)for a Matlab function filter(B,A,x)!!!
Thanks!
PS: Sorry for my English.
@Julián: A simple integrator can be a filter with transfer function H(z) = kz^-1/(1 – (1-k)z^-1)
% example matlab code
ip = ones(1,100);
k = 0.2;
op2 = filter([0 k],[1 -(1-k)],ip);
Hi,
could you please explain the frequency response code snippet given above in one of the posts. How does it differ for a decimation filter?
regards,
Samanvita
@samanvita: Whether its interpolation or decimation filter, both are rectangular filters in time domain, which has a sinc() shaped frequency response. The rectangular filters can be equivalently implemented using an integrator arm and a comb arm . In the case of differentiation filter, we have the comb arm after the downsampling (to save the delay line depth).
Hope this helps.
Hello Krishna,
Thanks for looking into the paper. I just wanted to point out that “N” has a major impact on the filter. As you have noticed, Eq(1) refers to a single integrator stage and Eq(2) refers to a single comb stage. The number of stages in the integrator and the number of stages in the comb section are equal. The only difference is that the comb section runs at a lower sampling rate.
Anyways, glad you were able to look into this paper. May be it’ll give you ideas for the future.
Regards,
Rohith
hello,
In this post krishna has worked on single stage Integrator and comb.
and its true that in Hogenauer’s paper – “An economical class of digital filters for decimation and interpolation” he said about multistage implementation.
As we increase the number of stages the image/alias rejection will improve.
Here in krishna blog N=10 only refers to the number of samples in T duration.
I hope this will help.
@Rohit: I downloaded the Hogenauer’s paper – “An economical class of digital filters for decimation and interpolation”
As I understand, he is just stating there can be N integrator stages with each having unity delay. See Eq (1) and Fig (1,2).
In our simple example, we are having only ONE integrator stage. Hope this explains.
Hello Krishna,
Thanks for the reply. I noticed that in the diagram too, which is where I got confused. The code and the diagram go together, but I am wondering whether the concept is right.
Here is a excerpt from Hogenauer’s original paper on CIC filters. Note that it mentions “N” stages for both integrator and comb sections.
“The integrator section of CIC filters consists of N ideal digital integrator stages operating at the high sampling rate, fs,. Each stage is implemented as a one-pole filter with a unity feedback coefficient. The comb section operates at the low sampling rate fs/R, where R is the integer rate change factor. This section consists
of N comb stages with a differential delay of M samples per
stage.”.
@Rohith: Its the comb stage which has the N delay element, integrator has only one delay. I am hoping that the figure above is self explanatory.
Hello Krishna,
I’m not sure if I completely follow the code for the CIC filter.
Does “N” refer to the number of stages? If so, then why is it that the integrator only has one stage?
Here is the code from the above post for CIC filter where the comb section follows the integrator section:
Thanks,
Rohith
% Implementing Cascaded Integrator Comb filter with the
% integrator section following the comb stage
N = 10;
delayBuffer = zeros(1,N);
intOut = 0;
xn = sin(2*pi*[0:.1:10]);
for ii = 1:length(xn)
% integrator
intOut = intOut + xn(ii);
% comb section
combOut = intOut – delayBuffer(end);
delayBuffer(2:end) = delayBuffer(1:end-1);
delayBuffer(1) = intOut;
y3n(ii) = combOut;
end
This is great! Thanks!
@Rudheesh: Thanks. You can also also look at the other posts and give your valuable feedback.
Yeah, am from Kerala…. though now its Bangalore which gives me the rice and sambar. 😉
Hi Krishna,
Thank you for the excellent article. You have simplified the concept in a way so that evryone can understand.
Keep up the good work.
By the way, are you from kerala??
@venkata : you can use the fdatool for designing both fir/iir low/high/band pass/stop filters in Matlab.
type fdatool on the matlab command line to invoke the gui.
can anyone got the code for designing theFIR lowpass filter in MATLAB
Dear Venkat,
Though it is long time ago you have posted. I just want to give you the code for fixed point FIR Lowpass filter in Matlab:
Fs = 1400; % Sampling Frequency
Fc =400; % Cutoff Frequency
N = 20; % Order of the Filter
n = 8; % Input word length i.e if ADC is 8 bit then use 8, if 12 bit then use %12,…and so on
CWL = 8; % Coeff word length must be >= to ‘n’ so i.e if n is 8 bit then use 8 or %>8, if 12 bit then use 12 or >12,…and so on
flag = ‘scale’; % Sampling Flag
% Create the window vector for the design algorithm.
win = rectwin(N+1);
% Calculate the coefficients using the FIR1 function.
b = fir1(N, Fc/(Fs/2), ‘low’, win, flag);
Hd = dfilt.dffir(b);
% Set the arithmetic property.
set(Hd, ‘Arithmetic’, ‘fixed’, …
‘CoeffWordLength’, CWL, …
‘CoeffAutoScale’, true, …
‘Signed’, true, …
‘InputWordLength’, n, …
‘inputFracLength’, 0, …
‘FilterInternals’, ‘FullPrecision’);
denormalize(Hd);
% plots the magnitude response of the filter by default. If you have %a signal %processing tool box then you can explore more on this plot
fvtool(Hd)
%**********************************************************************%
%***Below code is to convert double type coefficients to integer****%
%******Write filter coefficients to GUI Table/excel sheet**************%
%*********************************************************************%
read_coefficients = Hd.coeffs; %read_coefficients is structure type
conv_coefficients_CELL=struct2cell(read_coefficients);
conv_coefficients_MAT=cell2mat(conv_coefficients_CELL);
Coeff_MAX_Val=max(abs(conv_coefficients_MAT));
Integer_Coeff_Val=round(((2^(CWL-1)-1)*conv_coefficients_MAT/Coeff_MAX_Val));
xlswrite(‘Lowpass_Filter_Coefficients.xls’, (Integer_Coeff_Val)’);
Hope that will help.
Prashant.S
@Prashant: Thanks for the help.
@tulasi:
the ‘comb’ aspect in CIC filter corresponds to the frequency response of the ‘comb’ section. If you use matlab/octave and run the attached code snippet, you can see that frequency response of the section
y[n] = x[n] – x[n-16] looks like start-quote “The periodic zeros remind us of the teeth of a comb, hence the name, comb filter.” end-quote
clear all
close all
N = 16;
fs = 1;
[h1F f1] = freqz([1 zeros(1,N-1) -1],[1],1024,’whole’);
plot([-512:511]*fs/1024,abs(fftshift(h1F)),’b.-‘)
hold on
xlabel(‘frequency’)
ylabel(‘magnitude’); title(‘frequency response of comb section’)
Hope this answers your query#2.
For query#1, from a quick wiking, I found that comb generator is a source which can generate multiple harmonics of the same signal.
and query#3: generating waveform which is the sum of multiple harmonics of the same sinusoidal should be reasonably trivial, no? You can look at the OFDM posts.
HTH,
Krishna
ps. it is not a good idea to provide mobile phone numbers on public domain. hence i edited that out from the post
dear sir,
this is tulasi
am working on “comb generator” i know it basically under microwave product.
my basic doubt is 1) what is comb generator?
2) what is the difference between comb generator and comb filter?
3) i need matlab implementation of comb generator software code
thanking u
tulasi babu
hyderabad
Amazing blog post about le of Cascaded Integrator Comb filter in Matlab – DSP log. I enjoy this view!
@ priya
Background:
As you may have observed, the CIC filter is a recursive implementation of a moving average filter (let us say of length N). Typically, when interpolation by a factor I , we insert I-1 zeros inbetween the samples and then do a filtering to remove the aliases.
When doing interpolation, for efficient hardware implementation (i.e. to reduce the number of elements in the comb buffer), we can first do the comb (with N/I delay elements), insert I-1 zeros, then integrate. However, the effect is same as passing the I-1 zero inserted samples through a moving average filter of length N.
To answer your query:
To find the frequency response, you can either use fft() of the time domain impulse response, or use the freqz() function in Matlab. Both gives identical frequency response.
% simple example – matlab/octave
clear all
close all
N = 16;
fs = 1;
ht = ones(1,N);
h1F = fft(ht,1024);
[h2F f2] = freqz([1 zeros(1,N-1) -1],[1 -1],1024,’whole’);
plot([-512:511]*fs/1024,abs(fftshift(h1F)),’b.-‘)
hold on
plot([-512:511]*fs/1024,abs(fftshift(h2F)),’rx-‘)
xlabel(‘frequency’)
ylabel(‘magnitude’)
Did that help?
Krishna
how to plot cic filter frequency response in matlab with the code mentioned above for interpolation?
Yes, for notational simplicity I ignored the scaling factor 1/N. However, I do believe that you agree with the recursive implementation.
With the scaling factor,
y[n] = y[n-1] + (1/N)*(x[n] – x[n-N])
% simple matlab example:
ip = randn(1,100);
op1 = conv(ip,(1/16)*ones(1,16));
op2 = filter((1/16)*[1 zeros(1,15) -1],[1 -1],ip);
err = op1(1:100) – op2;
errdB = 10*log10(err*err’/length(err))
HTH,
Krishna
For moving average,
|Hf|
={1/N*[sin(pi*f*N)]/[sin(pi*f)]}
but for CIC
|Hf|
={[sin(pi*f*N)]/[sin(pi*f)]}
Why they are the same, as a scaling factor is there, 1/N ? thanks.