In this post, let us evaluate the impact of frequency offset resulting in Inter Carrier Interference (ICI) while receiving an OFDM modulated symbol. We will first discuss the OFDM transmission and reception, the effect of frequency offset and later we will define the loss of orthogonality and resulting signal to noise ratio (SNR) loss due to the presence of frequency offset. The analysis is accompanied by Matlab/Octave simulation scripts.
OFDM transmission
As discussed in the post on Understanding an OFDM transmission, for sending an OFDM modulated symbol, we use multiple sinusoidals with frequency separation is used, where
is the symbol period. The information
to be send on each subcarrier
is multiplied by the corresponding carrier
and the sum of such modulated sinusoidals form the transmit signal. Mathematically, the transmit signal is,
The interpretation of the above equation is as follows:
(a) Each information signal multiplies the sinusoidal having frequency of
.
(b) Sum of all such modulated sinusoidals are added and the resultant signal is sent out as .
OFDM reception
In an OFDM receiver, we will multiply the received signal with a bank of correlators and integrate over the period . The correlator to extract information send on subcarrier
is
.
The integral,
,
where
takes values from
till
.
Frequency offset
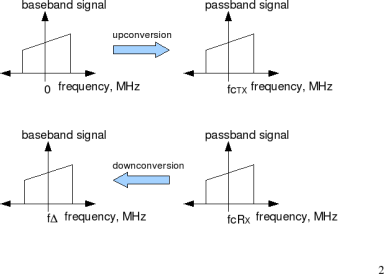
In a typical wireless communication system, the signal to be transmitted is upconverted to a carrier frequency prior to transmission. The receiver is expected to tune to the same carrier frequency for down-converting the signal to baseband, prior to demodulation.
Figure: Up/down conversion

However, due to device impairments the carrier frequency of the receiver need not be same as the carrier frequency of the transmitter. When this happens, the received baseband signal, instead of being centered at DC (0MHz), will be centered at a frequency , where
.
The baseband representation is (ignoring noise),
, where
is the received signal
is the transmitted signal and
is the frequency offset.
Effect of frequency offset in OFDM receiver
Let us assume that the frequency offset is a fraction of subcarrier spacing
i.e.
.
Also, for simplifying the equations, lets us assume that the transmitted symbols on all subcarriers,
The received signal is,
.
The output of the correlator for sub-carrier is,
.
For ,
The integral reduces to the OFDM receiver with no impairments case.
However for non zero values of , we can see that the amplitude of the correlation with subcarrier
includes
- distortion due to frequency offset between actual frequency
and the desired frequency
.
- distortion due to interference with other subcarriers with with desired frequency
. This term is also known as Inter Carrier Interference (ICI).
Simulation Model
Click here to download the Matlab/Octave script for computing RMS error with frequency offset. The script performs the following:
1. Generates an OFDM symbol with all subcarriers modulated with .
2. Introduce frequency offset and add noise to result in =30dB.
3. Perform demodulation at the receiver.
4. Find the difference between the desired and actual constellation.
5. Compute the rms value of error across all subcarriers.
6. Repeat this for different values of frequency offset.
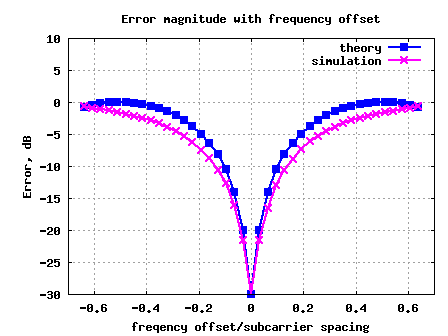
Figure: Error Magnitude vs frequency offset for OFDM
Observations
The theoretical results are computed by .
Quite likely the simulated results are slightly better than theoretical results because the simulated results are computed using average error for all subcarriers (and the subcarriers at the edge undergo lower distortion).
hidden morkov model and selected applications in speech recognition in mat lab implementation . in which i didn,t get an idea that can restructure the model by using matlab code.please can you help me to proceed to write a code in mat lab.and can u help me to modification in the existing hidden model in speech recognition so that we will get benefit .
@mahender: sorry, i have not studied much on the topic of speech recognition
I thank you for your course it s helpful
hello…
i am doing my PG project in ofdm communication…..can u plz give me the matlab code for ICI SELF CANCELLATION SCHEME IN OFDM SYSTEM according to IEEE 802.11a standard….or suggest some reference material…which will help me…..
thanks…..
@tejashri: I ‘ve not not studied that topic. For OFDM related posts, please checkout
https://dsplog.com/category/ofdm/
please Krishna i work the 4Pam OFDM AWGN code and the code not run i want ask you what wrong in the program my email:engkareem.aast@hotmail.com:
clc
clear all
nFFT = 64; % fft size
nDSC = 52; % number of data subcarriers
nBitPerSym = 52; % number of bits per OFDM symbol (same as the number of subcarriers for PAM)
nSym = 10^4; % number of symbols
N = 10^5; % number of symbols
alpha4pam = [-3 -1 1 3]; % 4-PAM alphabets
EbN0dB = [0:10]; % bit to noise ratio
EsN0dB = EbN0dB + 10*log10(nDSC/nFFT) + 10*log10(64/80); % converting to symbol to noise ratio
for ii = 1:length(EbN0dB)
% Transmitter
ipMod = randsrc(1,nBitPerSym*nSym,alpha4pam);
ipMod = reshape(ipMod,nBitPerSym,nSym).’
% Assigning modulated symbols to subcarriers from [-26 to -1, +1 to +26]
xF = [zeros(nSym,6) ipMod(:,[1:nBitPerSym/2]) zeros(nSym,1) ipMod(:,[nBitPerSym/2+1:nBitPerSym]) zeros(nSym,5)] ;
% Taking FFT, the term (nFFT/sqrt(nDSC)) is for normalizing the power of transmit symbol to 1
xt = (nFFT/sqrt(nDSC))*ifft(fftshift(xF.’)).’;
% Appending cylic prefix
xt = [xt(:,[49:64]) xt];
% Concatenating multiple symbols to form a long vector
xt = reshape(xt.’,1,nSym*80);
% Gaussian noise of unit variance, 0 mean
nt = 1/sqrt(2)*[randn(1,nSym*80) + j*randn(1,nSym*80)];
% Adding noise, the term sqrt(80/64) is to account for the wasted energy due to cyclic prefix
yt = sqrt(80/64)*xt + 10^(-EsN0dB(ii)/20)*nt;
% Receiver
yt = reshape(yt.’,80,nSym).’; % formatting the received vector into symbols
yt = yt(:,[17:80]); % removing cyclic prefix
% converting to frequency domain
yF = (sqrt(nDSC)/nFFT)*fftshift(fft(yt.’)).’;
yMod = yF(:,[6+[1:nBitPerSym/2] 7+[nBitPerSym/2+1:nBitPerSym] ]);
% demodulation
r = real(yt); % taking only the real part
ipHat(find(r= 2/sqrt(5))) = 3;
ipHat(find(r>=-2/sqrt(5) & r=0 & r<2/sqrt(5))) = 1;
% converting modulated values into bits
ipBitHat = (ipHat+3)/2;
ipBitHat = reshape(ipBitHat.',nBitPerSym,nSym).';
% counting the errors
nErr(ii) = size(find(ipBitHat – ipMod),2);
end
simBer = nErr/N;
theoryBer = 0.75*erfc(sqrt(0.2*(10.^(Es_N0_dB/10))));
close all
figure
semilogy(Es_N0_dB,theoryBer,'b.-');
hold on
semilogy(Es_N0_dB,simBer,'mx-');
axis([-3 20 10^-5 1])
grid on
legend('theory', 'simulation');
xlabel('Es/No, dB')
ylabel('bit Error Rate of 4 pam OFDM')
title('bit error probability curve for 4-PAM modulation')
@kareem: Are you getting zero BER in no noise case?
How are the bits getting converted to modulation symbols?
Hello,
Can you told me, how to simplify
sum(a^2)/sum(a)
where a is a vector of N complex variables.
@Ahmed: How about sum(a.^2)./sum(a) in matlab ? Note the dot (.)
hi krishna
find here with program for standard OFDM simulator in MATLAB
%%OFDM simulator
ep = [0 .15 .3 ];
% Es/No
EbNo=0:30;
% NS = number of OFDM symbols to transmit
NS = 100;
% Modulation type
modulation = ‘psk’;
M = 4
% N = number of carriers in OFDM symbol
N = 52;
% BPS = number of bits per OFDM symbol
BPS = N*log2(M);
% index for carriers in OFDM symbol
carriers = (1:52) + 2;
% IFFT size
ifftsize = 64;
% Input Bit Stream is normally Distributed
input_bit_stream = sign(randn(1,BPS*NS));
input_bit_stream(input_bit_stream == -1) = 0;
% PERFORM SERIAL TO PARALLEL CONVERSION
parallel_data = reshape(input_bit_stream, log2(M));
% PERFORM MODULATION
modulated_data = dmodce(parallel_data, 1, 1, modulation, M);
% CREATE OFDM SYMBOLS
disp(‘Transmitting OFDM symbols’)
%Normalize
%modulated_data = (modulated_data/max(abs(modulated_data)));
for ll= 1:length(ep)
for l=1:length(EsNo)
k = 1;
for n = 1:NS
ofdm_symbol = zeros(1,ifftsize);
% Map modulated data to FFT bins in OFDM symbol
ofdm_symbol(carriers) = modulated_data(k:k+51);
% Time Signal to transmit
tx_signal = ifft(ofdm_symbol,ifftsize);
% DOPPLER SHIFT
rx_signal = tx_signal.*exp((j*pi*ep(ll)/ifftsize)*(0:ifftsize-1));
noise = sqrt(1/(2*log2(M)*10^(EsNo(l)/10)))*(randn(1,64)+j*randn(1,64));
rx_signal = rx_signal + noise;
% FFT
received_ofdm = fft(rx_signal, ifftsize);
% Extract data from carriers in OFDM symbol
received_symbols(k:k+51) = received_ofdm(carriers);
k = k + 52;
end
% PERFROM DEMODULATION
received_data = ddemodce(received_symbols, 1, 1, modulation, M);
%PERFORM PARALLEL TO SERIAL CONVERSION
output_bit_stream = reshape(received_data, log2(M));
% CALCULATE BER
BER(ll,l)= sum(xor(input_bit_stream, output_bit_stream))/length(input_bit_stream);
end
end
===================================================
i am experiencing problem in reshape. if you can rectify then i will be highly oblige.
send me reply on my mail : nbnadoda@yahoo.co.in
@nanu: Am sure you will be able to identify the problem in reshape() yourself 🙂
I am surprised as well Krishna, its the non-linear dynamics of the laser. I am still analyzing now. thanks anyway
@Thavamaran: Ok, good luck
Krishna, thanks for the quick reply. I dont get your question on linearly varying phase? But the constellation always has 45 or 135 or 225 or 315 degree of phase shift, so it has about 90 degree difference between them.
Anyway symbol timing synch has a lot of method, which method can I look into, do you have any code referring to timing synch?
For receiver portion, im using correlator receiver, not PLL cause I feel its pointless cause correlator works extremely well for my back-to-back.
@Thavamaran: Not sure why you are seeing a fixed phase shift. Kinda surprising.
hello please I try to estimate frequency offset in mimo ofdm using pn sequences have you an exaples for matlab codes could help me i make acquistion and tracking please advise it’s important .thanks
@eng_dina: Sorry, I do not have the matlab codes.
Hi Krishna, this is my first post in your website. This is a very straight forward example. I have built my OFDM system and my back-to-back works perfectly fine. But when I perform optical OFDM, which is part of my work, at the receiver, the constellation point shifted by 45 degree, then I just compensate the phase, but end up I realize that its nonlinear phase shift.
But I dont think I have a problem with CFO, cause its ideal. Do you think I need timing symbol synchronization? Please advise. Thanks.
@Thavamaran: Are you having a linearly varying phase across subcarriers? If yes, it might be related to the symbol timing synchronization.
Hi krishna
Kindly tell me why are we doing this: theoryErr = (theoryErr-1);
Regards
Obaid
Thank you for replying, I will see the post then I will back to discuss you.
@Shaimaa: Ok
The simulated curve was around 50% and increased slightly as EbNo increases.
Is it necessary to compensate for frequency offset before demodulating the bpsk symbols as in Rayleigh fading channel??????????
@Shaimaa: Typically, receivers will have a circuit for compensating frequency offset prior to attempting demodulation. I have written a brief post on how to estimate frequency offset with short preamble defined in 802.11a
https://dsplog.com/2008/03/03/frequency-offset-estimation-using-80211a-short-preamble/
I added the code
% Adding frequency offset
xt = xt.*exp(j*2*pi*freqOffsetkHz_v*(1e3/20e6)*[0:length(xt)-1]);
with freqOffsetkHz_v values=10 or 20 kHz
in your script_ber_bpsk_ofdm then run the program but the simulated curve was so bad. Is that expected
@Shaimaa: If there is frequency error, then the intercarrier interference can result in poor BER. However, I have not done the simulations to see how much bad it can get.
hi…
what are the problems are occur in high PAPR?
@PRIYA: Power amplifier efficiency is comprimised
please reply my massege it’s really important
thanks
Hi krishna,
I hope you are doing fine and great. I have seen your code and its great. here you have supposed that all the input symbols are modulated like ak=1, if I am right for this reason you are generating all ones as the input i.e.
ipBit = ones(1,nBitPerSym*nSym) > 0.5; (kindly correct me if I am wrong)
My point is that when we generate random bits i.e. ones and zeros, then the simmulated error is higher than the theoretical error …
kindly help in this regard …
@invizible: Oh, is it. I have not tried that.
Idon’t try to simulte cfo for mimo system only but for mimo ofdm I propose a new scheme that targets MMIO OFDM systems which have unsynchronized oscillators such that CFO of individual paths have to be estimated separately. This scheme may also apply to OFDM systems with multi-user access. The new method, which is similar to Moose’s method, estimates the CFO by measuring the carrier phase difference between 2 identical successive training sequences embedded in the preambles. In order to make CFO estimates be more time efficient,I allow 2 transmitter antennas transmit their training sequence concurrently in every time period, except the first and the last period. I use Frank-Zadoff code with different phase shifts in the training sequences in different antennas. Due to the good correlation property of Frank-Zadoff code, it helps reduce the interference caused by the concurrent transmissions from other antennas.
please helpppppppppppppppppppppppp
please reply me it’s urgent Ineed the code it’s really important and thanks alot
@eng_dina: Good luck with you are algorithm investigation. Hope you have made the simulations and obtained satisfactory results.
Could you help me to find the theoretical BER of OFDM with Walsh-Hadamard over the multipath transmission
@Ahmed: Sorry, I do not have the required information
Idon’t try to simulte cfo for mimo system only but for mimo ofdm I propose a new scheme that targets MMIO OFDM systems which have unsynchronized oscillators such that CFO of individual paths have to be estimated separately. This scheme may also apply to OFDM systems with multi-user access. The new method, which is similar to Moose’s method, estimates the CFO by measuring the carrier phase difference between 2 identical successive training sequences embedded in the preambles. In order to make CFO estimates be more time efficient,I allow 2 transmitter antennas transmit their training sequence concurrently in every time period, except the first and the last period. I use Frank-Zadoff code with different phase shifts in the training sequences in different antennas. Due to the good correlation property of Frank-Zadoff code, it helps reduce the interference caused by the concurrent transmissions from other antennas.
cfo for mimo only but for mimo ofdm system
please helpppppppppppppppppppppppp
Idon’t try to simulte cfo for mimo system only but for mimo ofdm I propose a new scheme that targets MMIO OFDM systems which have unsynchronized oscillators such that CFO of individual paths have to be estimated separately. This scheme may also apply to OFDM systems with multi-user access. The new method, which is similar to Moose’s method, estimates the CFO by measuring the carrier phase difference between 2 identical successive training sequences embedded in the preambles. In order to make CFO estimates be more time efficient,I allow 2 transmitter antennas transmit their training sequence concurrently in every time period, except the first and the last period. I use Frank-Zadoff code with different phase shifts in the training sequences in different antennas. Due to the good correlation property of Frank-Zadoff code, it helps reduce the interference caused by the concurrent transmissions from other antennas.
cfo for mimo only but for mimo ofdm system
please helpppppppppppppppppppppppp
Idon’t try to simulte After examining some synchronization I propose a new scheme that targets MMIO OFDM systems which have unsynchronized oscillators such that CFO of individual paths have to be estimated separately. This scheme may also apply to OFDM systems with multi-user access. The new method, which is similar to Moose’s method, estimates the CFO by measuring the carrier phase difference between 2 identical successive training sequences embedded in the preambles. In order to make CFO estimates be more time efficient,I allow 2 transmitter antennas transmit their training sequence concurrently in every time period, except the first and the last period. I use Frank-Zadoff code with different phase shifts in the training sequences in different antennas. Due to the good correlation property of Frank-Zadoff code, it helps reduce the interference caused by the concurrent transmissions from other antennas.
cfo for mimo only but for mimo ofdm system
please helpppppppppppppppppppppppp
thanks for your your graet work
please I study for my master in frequency synchronization in mimo ofdm system but i have problem with the matlab code to simulate to find out if estimation of the CFO on one path is affected by the CFO values of the adjacent paths and examine the estimator accuracy in term of its mean and variance
please help me it’s urgent and necessary
f_max = f_Tofdm/(M_sub*T_s); % f_max =maximal Doppler frequency (Hz),M_sub*T_s = OFDM Symbol period (sec),
%f_ndopp = f_max*M_sub*T_s % Normalized Maximum Doppler Spread Freq.
% Area parameter
% ra Rural Area
% tu Typical Urban
% bu Bad Urban
% ht Hilly Terrain
% no no fading
AREA = ‘no’ ;
% start simulation loops
for ee = 1 : length(EcNo)
ee
[theo_fo_var, rfo_var, rfo] = FOE_mimo_fading(EcNo(ee), tfo_array, NTX, NRX, M_sub, N, f_max, AREA, T_s, model, L);
plot_theo_fo_var(:,:,ee)=theo_fo_var;
plot_rfo_var(:,:,ee)=rfo_var;
plot_theo_rfo(:,:,ee)=tfo_array;
plot_rfo(:,:,ee)=rfo;
end
% plot results
for ii_tx = 1 : NTX
for ii_rx = 1 : NRX
% rearrange array order for easier plotting
vect_plot_theo_rfo = permute(plot_theo_rfo(ii_tx,ii_rx, :), [2 3 1]);
vect_plot_rfo= permute(plot_rfo(ii_tx,ii_rx, :), [2 3 1] ) ;
vect_plot_theo_fo_var= permute(plot_theo_fo_var(ii_tx,ii_rx,:),[2 3 1]);
vect_plot_rfo_var= permute(plot_rfo_var(ii_tx,ii_rx, :), [2 3 1]);
%plot mean
figure;
plot(EcNo, vect_plot_theo_rfo, ‘:’ , ‘Linewidth’,2) ;
hold;
plot(EcNo, vect_plot_rfo,’o-‘,’MarkerSize’ , 6,’Linewidth’, 1) ;
grid on;
t_str=sprintf(‘New_ Theo and Est Freq Offset %s M=%d N=%d %dx%d path:tx%d-rx%d fo=%1.3f’,AREA,M_sub,N,NTX,NRX,ii_tx,ii_rx,tfo_array(ii_tx,ii_rx));
title(t_str);
xlabel(‘EcNo SNR range and step (in dB)’);
ylabel(‘Norm Freq Offset’) ;
legend(‘Theo’,’Est’,’Location’,’Northeast’);
% save graph
fstr=sprintf(‘new_m%d_%dx%dp%d%d_%s’,M_sub,NTX,NRX,ii_tx,ii_rx,AREA);
hgsave(fstr);
% plot variance
figure;
semilogy(EcNo, vect_plot_theo_fo_var,’:’,’Linewidth’,2);
hold;
semilogy(EcNo, vect_plot_rfo_var,’o-‘,’MarkerSize’,6,’Linewidth’,1);
grid on;
grid minor;
t_str=sprintf(‘New_ Est Var and CRLB %s M=%d N=%d %dx%d path:tx%d-rx%d fo=%1.3f’,AREA,M_sub,N,NTX,NRX,ii_tx,ii_rx,tfo_array(ii_tx,ii_rx));
title(t_str);
xlabel(‘EcNo (in dB)’);
ylabel(‘Variance’);
legend(‘CRLB’,’Est’,’Location’,’Northeast’);
% save graph
fstr=sprintf(‘new_y%d_%dx%dp%d%d_%s’,M_sub,NTX,NRX,ii_tx,ii_rx, AREA) ;
hgsave(fstr);
end
end
% rename variables for export
new_plot_theo_fo_var=plot_theo_fo_var;
new_plot_rfo_var=plot_rfo_var ;
new_plot_theo_rfo=plot_theo_rfo;
new_plot_rfo=plot_rfo;
% save all variables
fstr=sprintf(‘new_f%d_%dx%d_%s.mat’,M_sub,NTX,NRX,AREA);
save(fstr);
% save variables for plotting
fstr=sprintf(‘new_p%d_%dx%d_%s.mat’,M_sub,NTX,NRX,AREA);
save(fstr,’new_plot_theo_fo_var’,’new_plot_rfo_var’,’new_plot_theo_rfo’,’new_plot_theo_rfo’);
% end of file
and this is the core of the code
@eng_dina: How are you modeling the CFO for MIMO systems?
If all the chains have a common RF clock, then all the chains will have similar CFO and the estimate from all the chains can be combined to improve the accuracy of the CFO estimation.
If the chains have independent RF clock, then we need to estimate CFO on each chain independently.
thanks alot for your helpful work please I work in my master in frequency synchronization in mimo ofdm and I have problem in the matlab code try to examine the estimator accuracy in term of its mean and variance and find out if estimation of the CFO on one path is affected by the CFO values of the adjacent paths
Hello,
can You explain why is sample frequency (20e6) in the term freqOffsetkHz_v(ii)*(1e3/20e6) necessary ? We need delta_f so it shall be actually -200:200kHz and not delta_f*sample_time …
best regards
Hi krishna
Can you please provide any references (books or web links) for SNR loss calculations (analytical) for AWGN and dispersive channels.
Regards.
Obaid
Sir,
I want to find BER for 4QAM in OFDM using AWGN. If i take the difference between reciver’s demodulated symbols and actual symbols(at transmitter) and devide the difference by the length of actual symbols, can i get the BER?
Thanks.
Hello Sir!
i gone through above code.it is useful to understand ici. but i have queery that how to cancel ici due to phase offset due to local oscillator frequency offset.
will you please help me.
thank you.
Can i think, delay spread is equal to total number of multiple paths in the system
@r.kalidoss: Delay spread is computed using the amplitude of the taps and their delay values.
Hi there…for one more question..
ipBit = ones(1,nBitPerSym*nSym) > 0.5; % random 1’s and 0’s
if i change “ones” to “rand”, the result seems to have differences. Can you explain it?
Thanks very much 🙂
@cyrus:
With ak’s randomly distributed, the interference term slightly changes. How much difference did you see?
1.I would like to know that why we need to have 1e3 in the following expression.
% Adding frequency offset
xt = xt.*exp(j*2*pi*freqOffsetkHz_v(ii)*(1e3/20e6)*[0:length(xt)-1]);
2.As you mentioned about,choosing -5 to 5 as subcarriers outside that range has negligible interference.I still have a bit of confuse about it.Can i change to others values?
@cyrus:
1/ To convert kHz to Hz
2/ Sure, you can.
Hi there,
I’m a bit confused about the theorical results calculation..
theoryErr =sum(1./(j*2*pi*([-5:5]+delta)).*(exp(j*2*pi*([5:5]+delta))-1));
could someone explain to me please how ([-5:5]+delta) relates to (k-m+delta)? Well I of course get the delta part just not sure how -5:5 was chosen?
Would really appreciate any reply
T
@Treasa: I just chose -5 to 5 as subcarriers outside that range has negligible interference.
referring to last line of this post:
why the subcarriers at the edge undergo lower distortion ???
@Obaid: Well, at the edge there will be subcarriers only at the left or right and not both. Hence there will be lower interference.
Hi krishna,
thank you so much for ur help and posts in this website,
i am working on Next generation WLAN 802.11n Simulation.
I need ur help
i would like get the simulation for MIMO OFDM with MMSE equalizer .and also with MIMO OFDM STBC codes.
pls help me .i would greatful if you help me.
thank you once again.
Sk.khaja rasool.
Pls: do reply to this mail ID khajarasool_17@yahoo.com
@Khaja Rasool: Though I have not disucssed MIMO + OFDM or STBC + OFDM, I have discussed MIMO, STBC, and OFDM independently. You may refer
https://dsplog.com/tag/mimo
https://dsplog.com/tag/stbc
https://dsplog.com/tag/ofdm
Good luck.
Can i think, due to change of frequency i.e. m/T to m+q/T (Frequency offset) orthogonality of the signal change?
@kalidoss: Yes, you are right.
Krishna, Can we think frequency offset is due to doppler shift…..apart from carrier mismatch in the receiver….
@kalidoss: I have not discussed Doppler in this post. I guess the effect of Doppler might not be as simple to understand as is the case with frequency offset. I will write about Doppler soon.
First time i saw the frequency offset problem in OFDM with simple example.Its fine working. Then to how to mitigate this problem.
Any method available to solve this issue.
@kalidoss: You may checkout the post on Frequency offset estimation using 802.11a short preamble
https://dsplog.com/2008/03/03/frequency-offset-estimation-using-80211a-short-preamble/