Chi Square Random Variable

Jul 28th, 2008 @ 06:14 am › Krishna Sankar
↓ Skip to comments

While trying to derive the theoretical bit error rate (BER) for BPSK modulation in a Rayleigh fading channel, I realized that I need to discuss chi square random variable prior.

What is chi-square random variable?

Let there be $m$ independent and identically distributed Gaussian random variables $X_i$ with mean $0$ and variance $\sigma^2$ and we form a new random variable,

$Z = \sum_{i=1}^mX_i^2$ .

Then $Z$ is a chi square random variable with $m$ degrees of freedom.

There are two types of chi square distribution. The first is obtained when $X_i$ has a zero mean and is called central chi square distribution. The second is obtained when $X_i$ has a non-zero mean and is called non-central chi square distribution. Four our discussion, we will focus only on central chi square distribution.

PDF of chi-square random variable with one degree of freedom

Using the text in Chapter 2 of [DIGITAL-COMMUNICATION: PROAKIS] as reference.

The most simple example of a chi square random variable is

$Z =X^2$ ,

where
$X$ is a Gaussian random variable with zero mean and variance $\sigma^2$ .

The PDF of $X$ is
$p(x)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{\frac{-x^2}{2\sigma^2}}$ .

By definition, the cumulative distribution function (CDF) of $Z$ is
$\begin{eqnarray}F_Z(z) &= &P(Z\le z) = P(X^2 \le z)\\& = &P\left(|X|\le \sqrt{z}\right)\end{eqnarray}$ .

This simplifies to

$\begin{eqnarray}F_Z(z) = F_X\left(\sqrt{z}\right) - F_X\left(-\sqrt{z}\right)\end{eqnarray}$ .

Differentiating the above equation with respect to $z$ to find the probability density function,

$\begin{eqnarray}p_Z(z)& =&\frac{p_x(\sqrt{z})}{2\sqrt{z}} + \frac{p_z(-\sqrt{z})}{2\sqrt{z}}\\& = &\frac{1}{2\sqrt{z}}\frac{1}{\sqrt{2\pi \sigma^2}}\left(e^{\frac{-z}{2\sigma^2}}+e^{\frac{-z}{2\sigma^2}}\right)\end{eqnarray}$ .

Summarizing, the pdf of chi square random variable with one degree of freedom is,

$p_Z(z)=\frac{1}{\sqrt{2\pi z\sigma^2}}e^{\frac{-z}{2\sigma^2}}$ .

PDF of chi-square random variable with two degrees of freedom

Chi square random variable with 2 degrees of freedom is,

$Z =X^2+Y^2$ ,

where,
$X$ and $Y$ are independent Gaussian random variables with zero mean and variance $\sigma^2$ .

In the post on Rayleigh random variable, we have shown that PDF of the random variable $A$ ,

where $A=\sqrt{X^2 + Y^2}$ is

$p_A(a) = \frac{a}{{\sigma^2}}e^{\frac{-a^2}{2\sigma^2}},\ a\ge 0$ .

For our current analysis, we know that

$Z=A^2$ .

Differentiating both sides,

$dz=2ada$ .

Applying this to the above equation, pdf of chi square random variable with two degrees of freedom is,
$p_Z(z) = \frac{1}{{2\sigma^2}}e^{\frac{-z}{2\sigma^2}},\ z\ge 0$ .

PDF of chi-square random variable with m degrees of freedom

The probability density function is,

$p_Z(z) = \frac{1}{{2^{m/2}\sigma^m\Gamma(\frac{m}{2})}}z^{m/2-1}e^{\frac{-z}{2\sigma^2}},\ z\ge 0$ , where

the Gamma function $\Gamma(p)$ is defined as,

$\Gamma(p) = \int_0^{\infty}t^{p-1}e^{-t}dt,\ p \ge 0$ ,

$\Gamma(p) = (p-1)!$ p an integer > 0

$\Gamma(1/2) = \sqrt{\pi}$

$\Gamma(3/2) = \frac{1}{2}\sqrt{\pi}$ .

I do not know the proof for deriving the above equation. If any one of you know of good references, kindly let me know. Thanks.

Simulation Model

Just for your reference, Matlab/Octave simulation model performing the following is provided

(a) Generate chi square random variables having m=1, 2, 3, 4, 5 degrees of freedom

(b) Probability density function is computed and plotted

Click here to download: Matlab/Octave script for simulating PDF of chi square random variable

PDF of chi square random variable

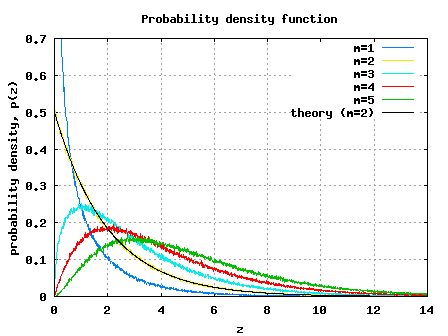
Figure: PDF of chi square random variable ( $\sigma^2$ =1)

Reference

[DIGITAL-COMMUNICATION: PROAKIS] Digital Communications, by John Proakis

Categories: Random Variables
Tags: chi square, pdf

8 Responses

Lealem

45 mos, 2 wks ago

I have seen the simulation code which u used to simulate a Rayleigh fading channel. But i would like u to ask a hit how to simulate a frequency selective Rayleigh fading channel for OFDM application. I think the above simulation out put is a flat Rayleigh fading.
Thank you!!!
Krishna Pillai

45 mos, 2 wks ago

@Lealem: As replied in
http://www.dsplog.com/2008/08/10/ber-bpsk-rayleigh-channel/#comment-1151
fajaru e

40 mos, 3 wks ago

sangat membantu dengan aadanya pembahasan soal spt ini. saya usul gimana, kalo qt bentuk komunitas lingkar studi khusus pembahasan soal seputar teknik elektro. dijamin banyak membantu. ditunggu info,thanx.
Krishna Pillai

40 mos, 3 wks ago

@fajaru: Can you please translate to english
Scr00m

34 mos, 3 wks ago

Few things in this world are free.
very few are nice too…
DSPlog.com is one of them
I thank you krishna for your efforts and sharing them worldwide.
Wish you good luck.
hope we will meet somewhere ..i wish
Krishna Pillai

34 mos, 2 wks ago

@Scr00m: Thanks. You may connect me to with my profile on LinkedIn.com http://www.dsplog.com/about/
sudhan

30 mos, 3 wks ago

Nice work. Could you please post the non-central chi square random variables, it is more interested since it is a distribution of Rician fading channel. You have provided all the performances based on Rayleigh fading channel. Could you please post BER of OFDM system over Rician fading channel. Thanks
sudhan
Krishna Sankar

30 mos, 3 wks ago

@sudhan: I will add that to the to-do list

Send a Message