This is the second post in the series discussing receiver diversity in a wireless link. Receiver diversity is a form of space diversity, where there are multiple antennas at the receiver. The presence of receiver diversity poses an interesting problem – how do we use ‘effectively‘ the information from all the antennas to demodulate the data. In the previous post, we discussed selection diversity. In this post, we will discuss equal gain combining (EGC). For the discussion, we will assume that the channel is a flat fading Rayleigh multipath channel and the modulation is BPSK.
Background
We use the same constraints as defined in the Selection Diversity post. Let me repeat the same.
1. We have N receive antennas and one transmit antenna.
2. The channel is flat fading – In simple terms, it means that the multipath channel has only one tap. So, the convolution operation reduces to a simple multiplication. For a more rigorous discussion on flat fading and frequency selective fading, may I urge you to review Chapter 15.3 Signal Time-Spreading from [DIGITAL COMMUNICATIONS: SKLAR]
3. The channel experienced by each receive antenna is randomly varying in time. For the receive antenna, each transmitted symbol gets multiplied by a randomly varying complex number
. As the channel under consideration is a Rayleigh channel, the real and imaginary parts of
are Gaussian distributed having mean
and variance
.
4. The channel experience by each receive antenna is independent from the channel experienced by other receive antennas.
5. On each receive antenna, the noise has the Gaussian probability density function with
with
and
.
The noise on each receive antenna is independent from the noise on the other receive antennas.
6. At each receive antenna, the channel is known at the receiver.
7. In the presence of channel , the instantaneous bit energy to noise ratio at
receive antenna is
. For notational convenience, let us define,
.
From the discussion on chi-square random variable, we know that, if is a Rayleigh distributed random variable, then
is a chi-squared random variable with two degrees of freedom. The pdf of
is
.
Equal Gain Combining (EGC)
On the receive antenna, equalization is performed at the receiver by dividing the received symbol
by the apriori known phase of
. The channel
is represented in polar form as
. The decoded symbol is the sum of the phase compensated channel from all the receive antennas.
where
is the additive noise scaled by the phase of the channel coefficient.
For demodulation, we use the classical definition i.e.
and
Note:
For PSK modulation schemes, the equalization by the phase of the channel coefficients suffice. However, for QAM case, we need to compensate for the amplitude also when equalizing. We are NOT discussing QAM case in this post.
Effective Eb/N0 with Equal Gain Combining
The equations listed below obtained from the article Receive diversity – Notes by Prof. Raviraj Adve.
In the presence of channel , the instantaneous bit energy to noise ratio at
receive antenna is
. For notational convenience, let us define,
.
The effective Eb/N0 with equal gain combining is the channel power accumulated over all receive chains, i.e.
.
The first term is chi-square random variable with degrees of freedom having mean value of
. Hence the first term reduces to,
.
The second term is a product of two Rayleigh random variables. The mean of Rayleigh random variable with variance is
. Hence the second term is,
.
Simplifying, the effective Eb/N0 with equal gain combining is,
.
Click here to download Matlab/Ocatve script for computing effective SNR with equal gain combining
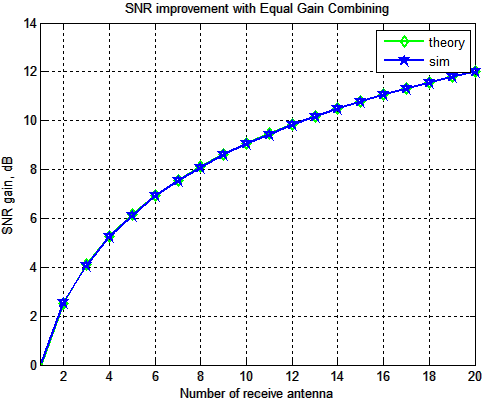
Figure : Gain in Eb/N0 with equal gain combining
Bit Error Rate with Equal Gain Combining
The IEEE paper [ZHANG97] discuss the BER computation with Equal Gain Combining. Since the proof is tedious (and I did not understand) I am just noting the final results.
With two receive antennas, the BER with equal gain combining is,
.
Matlab model for simulating BER with Equal Gain Combining
The Matlab/Octave script performs the following
(a) Generate random binary sequence of +1’s and -1’s.
(b) Multiply the symbols with the channel and then add white Gaussian noise.
(c) At the receiver, for each receive path, equalize by compensating with the known channel phase
(d) Accumulate the equalized symbols from all the receive paths
(d) Perform hard decision decoding and count the bit errors
(e) Repeat for multiple values of and plot the simulation and theoretical results.
Click here to download Matlab/Octave code for simulating BER for BPSK in Rayleigh fading channel with Equal Gain Combining
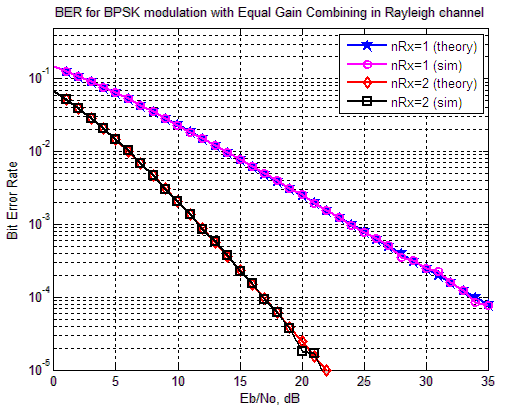
Figure: BER plot Receive Diversity with Equal Gain Combining
Can observe that the simulation results are in good agreement with the theoretical results. 🙂
Reference
[ZHANG97] Probability of error for equal-gain combiners over Rayleigh channels: some closed-form solutions Zhang, Q.T. Communications, IEEE Transactions on Volume 45, Issue 3, Date: Mar 1997, Pages: 270 – 273
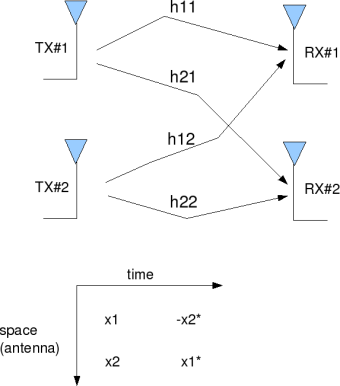
hy sir
i m undergraduate student.
my question is this while studying theory there are v.v.complicated equations as u have also written like effective Eb/No and for probability of error. where these equations are used. kindly can u help me
@sheby: The equations are mathematical representation of the underlying phenomena and is used to predict the performance. For eg, it will help us decide how much performance gain which we get, if we increase the number of antennas to 10, with out actually going ahead and building the device 🙂
Hello there!
I’m confused between Equal Gain Combining (EGC) and Square Law Combining (SLC) schemes.
Can you please elaborate the difference between them. As per my readings, literature says that they are different schemes, but I think that they are the same.
@Humayun: In equal gain combining, all the received copies of the signal are used with the same weight. However, in maximal ratio combining, the received copy with lower strength is given lower weightage.
Helps?
Hello Krishna,
thanks for this wonderful post on EGC. please is this code for GSM or CDMA system?
thanks.
@Arinze: This simulation does not specifically target GSM or CDMA system. It is for a simple flat fading case.
Hi Krishna,
In the program there is one line to do channel addition
sD = kron(ones(nRx(jj),1),s);
What is the significance of the above statement?? Cant we just multiply ‘h’ by ‘s’??
Kindly help.
@Tarun: No special significance. wanted to vectorize the matlab operation and the definition of sD helped to do h.*sD
Hello, when using EGC for PSK , is it necessary to divide the summed y with sum of channel gains at that moment from all receiving antennas? In that equation, you simply divide the phase term but the channel gains still remains there. Or maybe i’ve missed some assumptions?
@linkin8834: Maybe I did not do it because it is BPSK and the amplitude scaling does not matter.
Krishna,
In the first expression for effective Eb/No, shouldn’t it be the square of the sum of all h’s(power of the combined signal) rather than sum of squares(sum of the powers of individual signals)? With the expression that’s mentioned here, I don’t see how you get to the next expression.
@Sharad: In EGC, we make sure that the phases add constructively. Hence the sum of squares of powers makes sense. Agree?
Hello
I was trying to do a simulation for EGC using Monte Carlo simulation (not as shown above).
I followed the same steps, but the BER values still high (order of 10^-1). I don’t know why?
Please, can anybody help?
Thanks
Hello Sir,
I tried to implement the EGC using the Monte Carlo simulation and it didn’t work. Is there any explanation?
when trying to take the BER average for only two iterations I get answers of the order (10^-1) while when trying it only one time, I get very low values of BER which is what I want.
Thanks
Krishna,
Can you tell me if Equal Gain Combining is possible is time domain.
If so, can I implement it this way, that I simply sum up the number of chips that come in a Spreading Factor.
So, if SF = 4 and the received spread signal is,
x = [1 1 1 1 -1 -1 -1 1]
then,
EGC(x)@SF=4 = [4 -2]
Is this the correct approach?
Hello, I am using Equal Gain Combining to extract frequency domain diversity in MC-CDMA, but having problems with it.
At the transmitter, I modulate the binary data and repeat the symbols of each user on a given number of subcarriers, multiply it by a frequency domain spreading code (a row vector) and add the spread data of all users to have a composite signal.
At the receiver, for user 1, I multiply it by the same spreading code, and then use EGC to combine the modulation symbols.
I first want to test this algorithm without channel noise/impairments,
therefore, I think EGC will be
EGC = sum(RepSubcarDeSprdU1,1)
To get the sum of all symbols.
The problem, is the when I demodulate the result, there is a large error.
I must mention that this runs will for BPSK but shows errors for QPSK.
Any suggestions?
Thanks Krishna
@communications_engineer: Well, once you despread at the receiver, are you seeing the same information as was transmitted? Maybe to debug, try without spreading.
hey sir can we use egc for ml detector when using diversity mimo?? and how to use it…
@maya: Though I have not played with the equations, I believe it would be possible to use equal gain combining when there is a MIMO link with diversity. However, as you maybe aware, using Maximal Ratio Combining might be the most optimal approach.
Hi Sir,
i am working in MIMO systems. In the Equal Gain Combining’ code, the dephased output from N receive antennas are added and then the result is processed with hard decision decoding. My question is, should not the result of addition from N antennas be divided by the number of receive antennas (N here) before going for hard decision decoding?
@kunal: Yes, I agree. However, in BPSK modulation even if we do not do averaging, it does not matter as we are concerned only with the sign of the received symbol. Agree?
hello sir
sir currently i am involved with equal gain combing with 16-QAM.how to equalize with amplitude in QAM,please let me know.or any cite or book that i can get some reference about the amplitude equalization for EGC,16-QAM.awaiting for an immediate response.
@debabandana: You may refer to the post on Symbol Error Rate with 16-QAM in AWGN @
https://dsplog.com/2007/12/09/symbol-error-rate-for-16-qam/
Were you able to adapt that for 1 transmit 1 receieve Rayeligh channel scenario?
yes i have adapted for rayleigh channel…but in your program for EGC,you have done for BPSK modulation..for that amplitude eualization is not reqd..but for QAM amplitude equalization is reqd..i need that how to equalize amlitude with16-QAM ,EGC…
@debabandana: In the code, since it’s bpsk equalization is performed as y.*exp(-j*angle(h)). If we want to repmove the amplitude effects too, we can use:
(y.*exp(-j*angle(h)))./(abs(h))
Agree?
1.Is optimal combining technique the same as Ml detection at the receiver in case of receive diversity?
2.And in background noise limited case,Is the noise seen on each receiver the same,irrespective of area?So,if i have M receivers, total noise is M*noise variance of a single receiver(of area same as the total area of all M receivers)?or it depends upon area of receiver.
@Ankita: My responses
1. Maximal ratio combining is optimal in the case of receviver diversity. You can read bit more on MRC at
https://dsplog.com/2008/09/28/maximal-ratio-combining/
2. The thermal noise on each receiver depends on the receiver analog filter bandwidth. One can expect the analog filters for all the receivers to be the same.
Hope this helps.
Hi Pillai,
Even i fell the same.
Thanks for your reply.
If you find the better reasoning please let me know.
Thanks,
Sham Sunder K
@Sham Sunder K: Thats a difficult question, and I also do not know the answer. 🙁
The only reason which I can vaguely propose is that with multiple copies of the received symbol, the receiver chain with the higher snr dominates the ber.
Please do let know if you can think of a better argument.
Hi Pillai
Figure SNR improvement with EGC shows that we get approx 3dB gain with No. Rx Ant 2 when compared to one Rx Ant.
But If we see the BER curves of the same we get more than 3 dB gain.
What might be the reason??
Thanks & Regards,
Sham Sunder K
Hello Pillai,
Thank you very much for your answer,
In fact, I’m looking for some topics about full diversity (multiple transmit antennas for both sides…) with a combining technique…
Please, any help from your side will be helpful,
Kindest regards,
Nizar
Hello Pillai,
Thank you very much for your answer,
In fact, I’m looking for topics discussing multiple transmit antennas with EGC or MRC combining techniques (M transmitter antennas, N receiver antennas and a combining technique…).
Really, I don’t know the limitations of this case, but I’m trying to work on this aspect.
Kindest regards,
Nizar
@Nizar: Thanks.
I have not yet written topics dicussing multiple transmit antennas. Hope to do so in future, starting with Alamouti STBC coding for transmit diversity,
Hello Mr. Pallai,
Thank you very much for this clear and good analysis, it’s helpful and practical…
But, as well as I can remark this is only for receiver diversity, have any matlab code for both side diversity (N transmitter and M receiver antennas)?
Thanks by advance and best regards,
Nizar
I send them to your mail
and i said more details there.
Ali, I would like to discuss the simulation of MC-CDMA with different combining techniques. Contact me with my email i.e my name (withoutspace) @yahoo.com
@mohamadali: I have not yet taken up a detailed study of MC-CDMA to answer your request. However, I am hoping that you will be able to adapt the information given in this post to meet your requirement.
Btw, do you have a reference literature doing this comparison of MRC, ORC etc with MC-CDMA. If yes, kindly point me to the same. Let me study…
can u give me some tips to do OFDM MIMO for LTE
@Shabeer: Using the posts on OFDM (www.dsplog.com/tag/ofdm), it maybe reasonably easy to adapt for multiple antennas, different FFT sizes etc. Hope this helps. Good luck.
hello mr pillai
could you please show the performance of MRC, ORC and MMSE equalizers for MC-CDMA systems in rayleigh channels?