Oscillator phase noise

Oscillators are used in typical radio circuits to drive the mixer used for the up-conversion or down-conversion of the passband transmission. Ideally, the spectrum of the oscillator is expected to have an impulse at the frequency of oscillation with no frequency components else where. However the spectrum of practical oscillators do have spectrum skirts around the oscillation frequency caused due to phase noise. This post discuss about the phase noise of oscillator and the metrics used to specify it.

Oscillator spectrum

Consider the noisy output of an oscillator which has both amplitude noise $\alpha(t)$ and phase noise $\phi(t)$ .

$v(t) = A_c$1+\alpha(t)$\cos$\omega_c t + \phi\(t$\)$ .

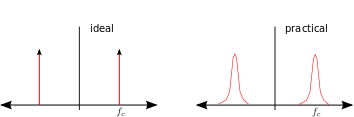
Figure : Spectrum of ideal and practical oscillators

Typically, any perturbations to the amplitude gets rejected by the oscillator circuit itself (due to the feedback path in the oscillator). However, any perturbation on the phase does not get corrected and it persists.

$v(t) = A_c\cos$\omega_c t + \phi\(t$\)$

Power spectral density of the phase $S_{\phi}$f$$

The noise on the phase can be modeled to have a a step function impulse response for a noise perturbation $n(t)$ , i.e.

$\begin{array}{lll}\phi (t)&=&u(t) \otimes n(t)&=&\int_{-\infty}^{+\infty}u$t-\tau$n$\tau$d\tau&=&\int_{-\infty}^{t}n$\tau$d\tau\end{array}$ .

The single sided power spectral density of the phase is,

$S_{\phi}$f$\approx\frac{S_n$f$}{$2\pi f$^2}$ .

This means that if :

a) $S_{n}$f$$ is caused by white noise, then $S_{\phi}$f$ \approx = \frac{1}{f^2}$

b) $S_{n}$f$$ is caused by flicker $\frac{1}{f}$ noise , then $S_{\phi}$f$ \approx = \frac{1}{f^3}$

and so on.

Power spectral density of the voltage signal $S_{v}$f$$

Given that the power spectral density of phase is difficult to observe directly, one might alternatively be interested in the power spectral density of the noisy oscillator out $v(t)$ .

Using the equations (9),(11) in Introduction to RF simulation and its application, Ken Kundert :

The power spectral density of $v(t)$ is,

$S_{v}$f$=\sum_{k=-\infty}^{k=+\infty}$\frac{a_k^2+b_k^2}{2}$\frac{ck^2f_c^2}{c^2\pi^2k^4f_c^4+$f-kf_c$^2}$ ,

where

$a_k,\ b_k$ are Fourier coefficients of $v(t)$ and $c$ is a constant.

Given that only frequencies at $f_c$ is needed, this simplifies to

$S_{v}$f$=\frac{a_1^2+b_1^2}{2}\frac{cf_c^2}{c^2\pi^2f_c^4+$f-f_c$^2}$ .

Substituting $f_b=c\pi f_c^2$ , the equation simplifies to,

$S_{v}$f$=\frac{a_1^2+b_1^2}{2\pi}\frac{f_b}{f_b^2+$f-f_c$^2}$ .

Note : The spectrum follows the Lorentzian function

It is a typical metric to report the single side band phase noise power to the power of the carrier and represent as,

$\mathcal{L}$f$=\frac{\frac{a_1^2+b_1^2}{2\pi}\frac{f_b}{f_b^2+$f-f_c$^2}}{\frac{a_1^2+b_1^2}{2}}=\frac{1}{\pi}\frac{f_b}{f_b^2+$f-f_c$^2}$ .

From Section 10.8 in Microwave Circuit Design Using Linear and Nonlinear Techniques, George D. Vendelin, Anthony M. Pavio, Ulrich L. Rohde

$\mathcal{L}$f$$ is the ratio of noise power in 1Hz bandwidth (BW) at offset $f$ from carrier to carrier signal power.

Typically $\mathcal{L}$f$$ is expressed in dBc/Hz i.e deciBels relative to carrier per Hertz. As expected, having a higher phase noise in the signal does not increase the total power. A signal with higher phase noise will have lesser power near $f_c$ and will be having a wide spectrum around the carrier. Conversely, a signal with lower phase noise has a sharper peak at the carrier with less skirts.

It can be shown that the integral of $\mathcal{L}$f$$ over all frequencies result in unity.

$\int_{-\infty}^{+\infty}\mathcal{L}$f$df=\frac{1}{\pi}\int_{-\infty}^{+\infty}\frac{f_b}{f_b^2+$f-f_c$^2}df=\frac{1}{\pi}\int_{-\pi /2}^{+\pi /2}\frac{1}{f_b}\frac{f_b\sec^2\theta}{$1+\tan^2\theta$}d\theta=1$ .

Matlab example

The following code snippet plots the $\mathcal{L}$f$$ for $f_c=500$ and three different values of $c$ .

close all; clear all;
fc = 500;
f  = [1:.1:1000];

c1  = 2*1e-5; f1b = c1*pi*fc^2; L1f = 1/pi*f1b./(f1b^2 + (f-fc).^2);
c2  = 1e-5; f2b = c2*pi*fc^2; L2f = 1/pi*f2b./(f2b^2 + (f-fc).^2);
c3  = 0.5*1e-5; f3b = c3*pi*fc^2; L3f = 1/pi*f3b./(f3b^2 + (f-fc).^2);

plot(f,L1f,'bs-'); hold on;
plot(f,L2f,'mp-'); plot(f,L3f,'gx-');
xlabel('freq, Hz'); ylabel('L(f)');
title('L(f), ratio of noise power to carrier power');
axis([300 700 0 0.09]); grid on;
legend('c=2e-5','c=1e-5', 'c=0.5e-5');

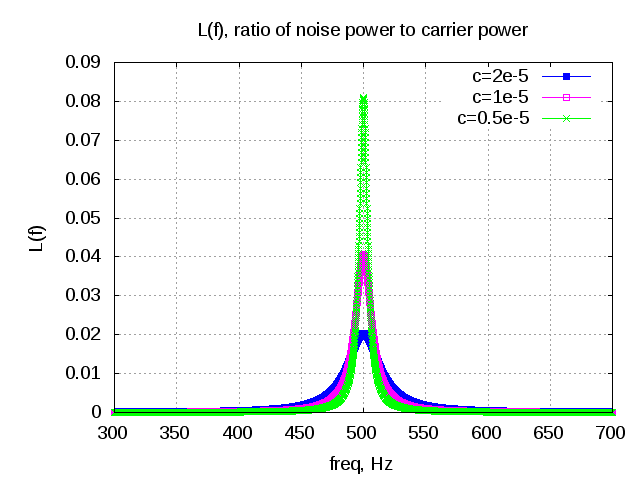
Figure: Plot of the noise power to carrier power for different values of c

As can be seen from the above figure, for higher values of $c$ , the spectrum becomes wider with lesser amplitude in the main lobe of the spectrum. Note that a wider main lobe does not increase the total power of the carrier.

The power spectral density can be approximated as,

$\mathcal{L}$f$=\{\begin{array}{lr}\frac{1}{\pi f_b},&f\rightarrow f_c\\\frac{1}{2\pi f_b},&f=f_c+f_b\\\frac{f_b}{\pi f^2},&f\gg f_c+f_b\end{array}$ .

The spectrum of $\mathcal{L}$f$$ with choosing $f_b=\frac{1}{\pi}$ and dowconverting with an ideal osciallator tuned to $f_c$ is plotted below.

clear all;
fc = 500; f  = [0.01:.01:100];
fb = 1/pi;
Lf = 1/pi*fb./(fb^2 + (f-fc+fc).^2);
Lf_approx = 1/pi*fb./(f-fc+fc).^2;

semilogx((f),10*log10(Lf),'bs-'); hold on;
semilogx((f),10*log10(Lf_approx),'rp-');
xlabel('freq, Hz'); ylabel('L(f), dBc/Hz');
title('L(f), ratio of noise power to carrier power');
legend('L(f)','L(f) approx');
axis([0.01 100 -50 10]); grid on;

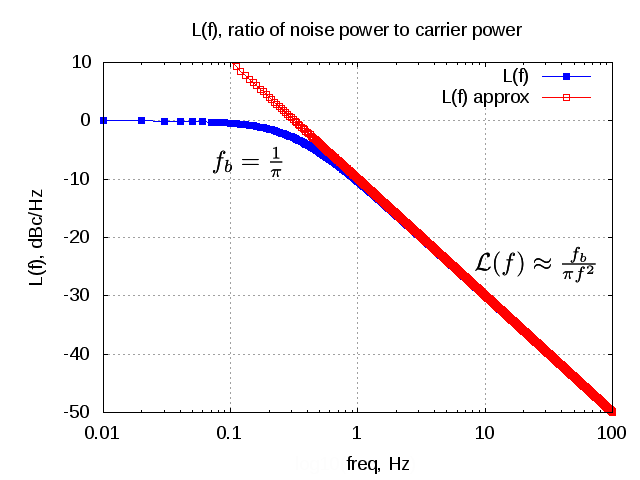
Figure : Normalized power spectral density

Relationship between ${\mathcal{L}$f$}$ and ${S_{\phi}$f$}$

It can be seen that ${S_{\phi}$f$}$ grows unbounded as frequency tends towards the carrier frequency, i.e.

${S_{\phi}$f$}\rightarrow\infty$ as $f\rightarrow f_c$ .

However, the spectrum of the voltage signal is bounded.

$\begin{array}S_{v}$f$=\frac{a_1^2+b_1^2}{2\pi f_b}, &&&f\rightarrow f_c\end{array}$

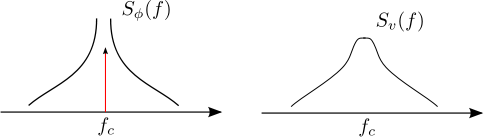
Figure : Oscillator phase and voltage spectrum

From equation (16) in Introduction to RF simulation and its application, Ken Kundert, for $f\gg f_c + f_b$ ,

$\mathcal{L}$f$=\frac{1}{2}S_\phi$f$$ .

Note :

Did not fully appreciate the physical significance of having this relationship true only for frequencies $f\gg f_c + f_b$ . Anyhow a small proof for the above relationship assuming that the phase noise signal is a sinusoidal is given below.

Consider that the phase noise signal $\phi(t)$ is a sinusoidal i.e.

$\phi(t)=A_m\sin(\omega_m t\)$ .

The spectral density of the phase is,

$S_{\phi}$f$=E\[\phi^2$t$\]=\frac{A^2_m}{2}$ .

The noisy carrier signal is,

$\begin{array}{lll}c_n(t)&=&A_c\cos$\omega_c t + A_m\sin\(\omega_m t$\)\\&=&A_c\cos$\omega_ct$\cos$A_m\sin(\omega_mt$\)-A_c\sin$2\pi f_ct$\sin$A_m\sin(\omega_mt$\)\end{array}$

Assuming $A_m\sin(\omega_m t\)$ is small,

$\cos$A_m\sin(\omega_mt$\) \approx 1$ and

$\sin$A_m\sin(\omega_mt$\) \approx A_m\sin(\omega_mt\)$ .

With this the equation simplifies to,

$\begin{array}{lll}c_n(t)&=&A_c\cos$\omega_ct$-A_c\sin$\omega_ct$A_m\sin(\omega_mt\)\\&=&A_c\cos$\omega_ct$-\frac{A_cA_m}{2}\cos$\(\omega_c-\omega_m$t\)+\frac{A_cA_m}{2}\cos$\(\omega_c+\omega_m $t\)\end{array}$ .

The ratio of the single side band power to the carrier power is,

$\mathcal{L}$f$=\frac{$\frac{\(\frac{A_cA_m}{2}$^2}{2}\)}{$\frac{A^2_c}{2}$}=\frac{A^2_m}{4}=\frac{1}{2}S_\phi$f$$ .

Matlab script (phase modulation)

% Matlab script showing the spectrum of a phase modulated carrier
clear all; close all
n_fft = 1024;
fc = 50; fs = 1024;
ts = [0:1023]/fs;
Ac = 2; Am = 0.2; fm = 10;
ct   = Ac*cos(2*pi*fc*ts); % carrier
phit = Am*sin(2*pi*fm*ts); % modulating signal
vt   = Ac*cos(2*pi*fc*ts + phit); % phase modulated carrier
cf = 1/(n_fft)*fft(ct,n_fft);
vf = 1/(n_fft)*fft(vt,n_fft);
plot([-512:511]*fs/1024,10*log10(abs(fftshift(vf)).^2),'mx-')
hold on;
plot([-512:511]*fs/1024,10*log10(abs(fftshift(cf)).^2),'bs-');
axis([0 100 -50 10]); grid on;
xlabel('freq, Hz');
ylabel('power spectral density, dB')
title('spectrum plot');
legend('phase modulated carrier','un modulated carrier');

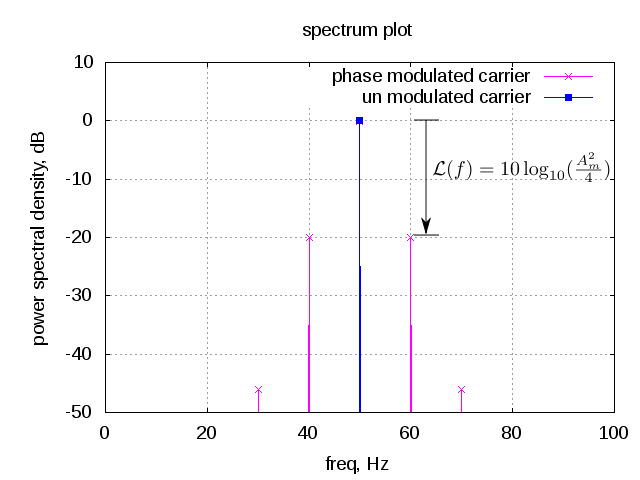
Figure : Phase modulated carrier

For the above example, with respect to the carrier the side lobes at $f_m$ are $\mathcal{L}$f$=10\log_{10}${A_m^2/4}$=-20dB$ down. There are more side lobes at $2f_m$ and further multiples of $f_m$ , which can be ignored assuming that $A_m$ is small.

Summary

a) The power spectral density of phase is related to the spectrum of the noise perturbation as

$S_{\phi}$f$\approx\frac{S_n$f$}{$2\pi f$^2}$

b) Phase noise typically can be modeled to have a Lorentzian spectrum and the phase noise relative to the carrier is typically $\mathcal{L}$f$$ is expressed in dBc/Hz i.e deciBels relative to carrier per Hertz

c) The power spectral density of the phase ${S_{\phi}$f$}$ and $\mathcal{L}$f$$ are related as,

${\begin{array}\mathcal{L}$f$=\frac{1}{2}S_\phi$f$,&&& f\gg f_c + f_b\end{array}}$ .

References:

a) Introduction to RF simulation and its application, Ken Kundert, Version 2, 23 April 2003

b) wiki entry on Lorentzian function

c) Microwave Circuit Design Using Linear and Nonlinear Techniques, George D. Vendelin, Anthony M. Pavio, Ulrich L. Rohde

d) Pulikkoonattu, R. (June 12, 2007), Oscillator Phase Noise and Sampling Clock Jitter, Tech Note, Bangalore, India: ST Microelectronics, retrieved March 29, 2012

Migrated to Amazon EC2 instance (from shared hosting)

GATE-2012 ECE Q28 (electromagnetics)

Image Rejection Ratio (IMRR) with transmit IQ gain/phase imbalance

GATE-2012 ECE Q15 (communication)

GATE-2012 ECE Q7 (digital)

GATE-2012 ECE Q13 (circuits)

Oscillator phase noise

Oscillator spectrum

Power spectral density of the phase $S_{\phi}\(f\)$

Power spectral density of the voltage signal $S_{v}\(f\)$

Relationship between ${\mathcal{L}\(f\)}$ and ${S_{\phi}\(f\)}$

Summary

References:

4 thoughts on “Oscillator phase noise”

Leave a Reply Cancel reply

Oscillator spectrum

Power spectral density of the phase

Power spectral density of the voltage signal

Relationship between and

Summary

References:

4 thoughts on “Oscillator phase noise”

Leave a Reply Cancel reply

Related Articles

Power spectral density of the phase $S_{\phi}\(f\)$

Power spectral density of the voltage signal $S_{v}\(f\)$

Relationship between ${\mathcal{L}\(f\)}$ and ${S_{\phi}\(f\)}$