MIMO

Six equalizers for V-BLAST

Krishna Sankar16 years ago12 years ago6711 mins

In the past, we had discussed several posts on two transmit two receive MIMO communication, where the transmission was based on V-BLAST. The details about V-BLAST can be read from the landmark paper V-BLAST: An architeture for realizing very high data rates over the rich scattering wireless channel – P. W. Wolniansky, G. J. Foschini, G. D. Golden, R. A. Valenzuela. We will assume that the channel is a flat fading Rayleigh multipath channel and the modulation is BPSK.

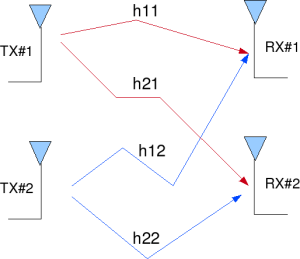
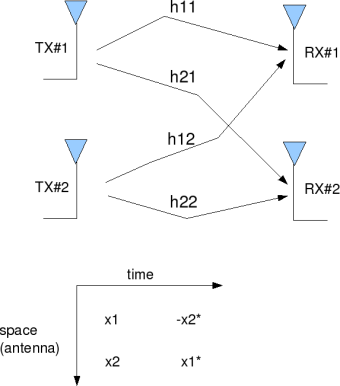
Figure: 2 transmit 2 receive MIMO channel

V-BLAST transmission for 2×2 MIMO channel

In a 2×2 MIMO channel, probable usage of the available 2 transmit antennas can be as follows:

1. Consider that we have a transmission sequence, for example ${x_1, x_2, x_3, \ldots, x_n }$

2. In normal transmission, we will be sending $x_1$ in the first time slot, $x_2$ in the second time slot, $x_3$ and so on.

3. However, as we now have 2 transmit antennas, we may group the symbols into groups of two. In the first time slot, send $x_1$ and $x_2$ from the first and second antenna. In second time slot, send $x_3$ and $x_4$ from the first and second antenna, send $x_5$ and $x_6$ in the third time slot and so on.

4. Notice that as we are grouping two symbols and sending them in one time slot, we need only $\frac{n}{2}$ time slots to complete the transmission – data rate is doubled ! 🙂

5. This forms the simple explanation of a probable MIMO transmission scheme with 2 transmit antennas and 2 receive antennas.

Other Assumptions

1. The channel is flat fading – In simple terms, it means that the multipath channel has only one tap. So, the convolution operation reduces to a simple multiplication. For a more rigorous discussion on flat fading and frequency selective fading, may I urge you to review Chapter 15.3 Signal Time-Spreading from [DIGITAL COMMUNICATIONS: SKLAR]

2. The channel experience by each transmit antenna is independent from the channel experienced by other transmit antennas.

3. For the $i^{th}$ transmit antenna to $j^{th}$ receive antenna, each transmitted symbol gets multiplied by a randomly varying complex number $h_{j,i}$ . As the channel under consideration is a Rayleigh channel, the real and imaginary parts of $h_{j,i}$ are Gaussian distributed having mean $\mu_{h_{j,i}=0$ and variance $\sigma^2_{h_{j,i}}=\frac{1}{2}$ .

4. The channel experienced between each transmit to the receive antenna is independent and randomly varying in time.

5. On the receive antenna, the noise $n$ has the Gaussian probability density function with

$p(n) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{\frac{-(n-\mu)^2}{2\sigma^2}$ with $\mu=0$ and $\sigma^2 = \frac{N_0}{2}$ .

7. The channel $h_{j,i}$ is known at the receiver.

System Model

The received signal on the first receive antenna is,

$y_1 =h_{1,1}x_1 + h_{1,2}x_2 + n_1 = [h_{1,1}\ h_{1,2}] \left[\begin{eqnarray}x_1 \\ x_2 \end{eqnarray}\right]+n_1$ .

The received signal on the second receive antenna is,

$y_2 = h_{2,1}x_1 + h_{2,2}x_2 + n_2 = [h_{2,1}\ h_{2,2}] \left[\begin{eqnarray}x_1 \\ x_2\end{eqnarray}\right]+n_2$ .

where

$y_1$ , $y_2$ are the received symbol on the first and second antenna respectively,

$h_{1,1}$ is the channel from $1^{st}$ transmit antenna to $1^{st}$ receive antenna,

$h_{1,2}$ is the channel from $2^{nd}$ transmit antenna to $1^{st}$ receive antenna,

$h_{2,1}$ is the channel from $1^{st}$ transmit antenna to $2^{nd}$ receive antenna,

$h_{2,2}$ is the channel from $2^{nd}$ transmit antenna to $2^{nd}$ receive antenna,

$x_1$ , $x_2$ are the transmitted symbols and

$n_1,\ n_2$ is the noise on $1^{st}, 2^{nd}$ receive antennas.

We assume that the receiver knows $h_{1,1}$ , $h_{1,2}$ , $h_{2,1}$ and $h_{2,2}$ . The receiver also knows $y_1$ and $y_2$ . The unknown s are $x_1$ and $x_2$ . Two equations and two unknowns. Can we solve it? Answer is YES. 🙂

For convenience, the above equation can be represented in matrix notation as follows:

$\begin{eqnarray}\left[\begin{eqnarray}y_1 \\ y_2\end{eqnarray}\right] & = & {\left[\begin{array}{cc}h_{1,1}& h_{1,2} \\h_{2,1}&h_{2,2}\end{array}\right]}\left[\begin{eqnarray}x_1 \\ x_2 \end{eqnarray}\right]+\left[\begin{eqnarray}n_1\\n_2 \end{eqnarray}\right]\end{eqnarray}$ .

Equivalently,

$\mathbf{y} = \mathbf{H}\mathbf{x} + \mathbf{n}$

Receiver structures

MIMO with Zero Forcing Equalization

The zero forcing approach tries to find a matrix $\mathbf{W}$ which satisfies $\mathbf{WH=I}$ . The Zero Forcing (ZF) linear detector for meeting this constraint is given by,

$\mathbf{W}=\mathbf{(H^HH)^{-1}H^H}$ .

MIMO with MMSE Equalization

The Minimum Mean Square Error (MMSE) approach tries to find a coefficient $\mathbf{W}$ which minimizes the criterion,

$E\left\{ \mathbf{\left[Wy-x\right]\left[Wy-x\right]}^H\right\}$ .

Solving,

$\mathbf{W=\left[H^HH+N_0I\right]}^{-1}\mathbf{H}^H$ .

Zero Forcing Equalization with Successive Interference Cancellation

Using the Zero Forcing (ZF) equalization approach described above, the receiver can obtain an estimate of the two transmitted symbols $x_1$ , $x_2$ , i.e.

$\left[\begin{array}\hat{x}_1\\\hat{x}_2\end{array}\right] = \mathbf{(H^HH)^{-1}H^H}\left[\begin{array}y_1\\y_2\end{array}\right]$ .

Take one of the estimated symbols (for example $\hat{x}_2$ ) and subtract its effect from the received vector $y_1$ and $y_2$ , i.e.

$\left[\begin{array}r_1\\r_2\end{array}\right] = \left[\begin{array}{ccl}y_1 &- & h_{1,2}&\hat{x}_2\\y_2 & - & h_{2,2}&\hat{x}_2\end{array}\right] = \left[\begin{array}{clc}h_{1,1}&x_1 &+ &n_1 \\ h_{2,1}&x_1 &+ &n_2\end{array}\right]$ .

Expressing in matrix notation,

$\left[\begin{array}r_1\\r_2\end{array}\right] = \left[\begin{array} h_{1,1}&amp\\h_{2,1}\end{array}\right]x_1 + \left[\begin{array}n_1\\n_2\end{array}\right]$ ,

$\mathbf{r} = \mathbf{h}x_1+\mathbf{n}$

The above equation is same as equation obtained for receive diversity case. Optimal way of combining the information from multiple copies of the received symbols in receive diversity case is to apply Maximal Ratio Combining (MRC).

The equalized symbol is,

$\hat{\mathbf{x}}_1 = \frac{\mathbf{h}^H\mathbf{r}}{\mathbf{h}^H\mathbf{h}}$ .

This forms the simple explanation for Zero Forcing Equalizer with Successive Interference Cancellation (ZF-SIC) approach.

Zero Forcing Equalization with Optimally ordered Successive Interference Cancellation

In classical Successive Interference Cancellation, the receiver arbitrarily takes one of the estimated symbols, and subtract its effect from the received symbol $y_1$ and $y_2$ . However, we can have more intelligence in choosing whether we should subtract the effect of $\hat{x}_1$ first or $\hat{x}_2$ first. To make that decision, let us find out the transmit symbol (after multiplication with the channel) which came at higher power at the receiver. The received power at the both the antennas corresponding to the transmitted symbol $x_1$ is,

$P_{x_1}=|h_{1,1}|^2 + |h_{2,1}|^2$ .

The received power at the both the antennas corresponding to the transmitted symbol $x_2$ is,

$P_{x_2}=|h_{1,2}|^2 + |h_{2,2}|^2$ .

If $P_{x_1}>P_{x_2}$ then the receiver decides to remove the effect of $\hat{x}_1$ from the received vector $y_1$ and $y_2$ and then re-estimate $\hat{x}_2$ . Else if $P_{x_1} \le P_{x_2}$ the receiver decides to subtract effect of $\hat{x}_2$ from the received vector $y_1$ and $y_2$ , and then re-estimate $\hat{x}_1$ .

MMSE equalization with optimaly ordered Successive Interference Cancellation

Using the Minimum Mean Square Error (MMSE) equalization, the receiver can obtain an estimate of the two transmitted symbols $x_1$ , $x_2$ , i.e.

$\left[\begin{array}\hat{x}_1\\\hat{x}_2\end{array}\right] = \mathbf{(H^HH+N_0I)^{-1}H^H}\left[\begin{array}y_1\\y_2\end{array}\right]$ .

If $P_{x_1}>P_{x_2}$ then the receiver decides to remove the effect of $\hat{x}_1$ from the received vector $y_1$ and $y_2$ $\hat{x}_2$ . Else if $P_{x_1} \le P_{x_2}$ the receiver decides to subtract effect of $\hat{x}_2$ from the received vector $y_1$ and $y_2$ , and then re-estimate $\hat{x}_1$ .

Once the effect of either $\hat{x}_1$ or $\hat{x}_2$ is removed, the new channel becomes a one transmit antenna, 2 receive antenna case and the symbol on the other spatial dimension can be optimally equalized by Maximal Ratio Combining (MRC).

MIMO with ML equalization

The Maximum Likelihood receiver tries to find $\hat{\mathbf{x}}$ which minimizes, $\mathbf{J} = \left| \mathbf{y} - \mathbf{H}\mathbf{\hat{x}} \right|^2$

$\mathbf{J} = \left|\begin{eqnarray}\left[\begin{eqnarray}y_1 \\ y_2\end{eqnarray}\right] & - & {\left[\begin{array}{cc}h_{1,1}& h_{1,2}\\ h_{2,1}&h_{2,2}\end{array}\right]}\left[\begin{eqnarray}\hat{x}_1 \\ \hat{x}_2 \end{eqnarray}\right]\end{eqnarray} \right|^2$

Since the modulation is BPSK, the possible values of $x_1$ is +1 or -1 Similarly $x_2$ also take values +1 or -1. So, to find the Maximum Likelihood solution, we need to find the minimum from the all four combinations of $x_1$ and $x_2$ .

$\mathbf{J_{+1,+1}} = \left|\begin{eqnarray}\left[\begin{eqnarray}y_1 \\ y_2\end{eqnarray}\right] & - & \left[\begin{array}{cc}h_{1,1}& h_{1,2}\\ h_{2,1}&h_{2,2}\end{array}\right]\left[\begin{eqnarray}+1 \\ +1 \end{eqnarray}\right]\end{eqnarray} \right|^2$

$\mathbf{J_{+1,-1}} = \left|\begin{eqnarray}\left[\begin{eqnarray}y_1 \\ y_2\end{eqnarray}\right] & - & \left[\begin{array}{cc}h_{1,1}& h_{1,2}\\ h_{2,1}&h_{2,2}\end{array}\right]\left[\begin{eqnarray}+1 \\ -1 \end{eqnarray}\right]\end{eqnarray} \right|^2$

$\mathbf{J_{-1,+1}} = \left|\begin{eqnarray}\left[\begin{eqnarray}y_1 \\ y_2\end{eqnarray}\right] & - & \left[\begin{array}{cc}h_{1,1}& h_{1,2}\\ h_{2,1}&h_{2,2}\end{array}\right]\left[\begin{eqnarray}-1 \\ +1 \end{eqnarray}\right]\end{eqnarray} \right|^2$

$\mathbf{J_{-1,-1}} = \left|\begin{eqnarray}\left[\begin{eqnarray}y_1 \\ y_2\end{eqnarray}\right] & - & \left[\begin{array}{cc}h_{1,1}& h_{1,2} \\ h_{2,1}&h_{2,2}\end{array}\right]\left[\begin{eqnarray}-1 \\ -1 \end{eqnarray}\right]\end{eqnarray} \right|^2$

The estimate of the transmit symbol is chosen based on the minimum value from the above four values i.e

if the minimum is $\mathbf{J_{+1,+1} \Rightarrow [1 \ 1 ]$ ,

if the minimum is $\mathbf{J_{+1,-1} \Rightarrow [1 \ 0 ]$ ,

if the minimum is $\mathbf{J_{-1,+1} \Rightarrow [0 \ 1 ]$ and

if the minimum is $\mathbf{J_{-1,-1} \Rightarrow [0 \ 0 ]$ .

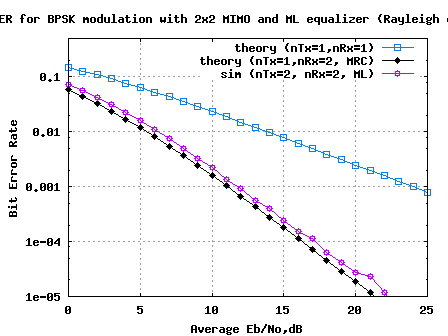
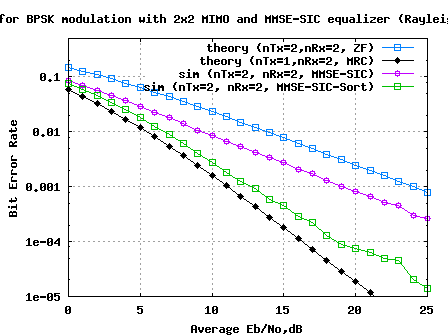
Simulation Results

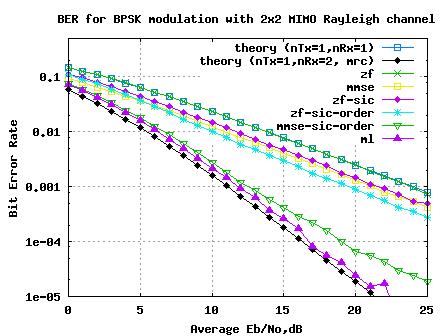
The plot embedded below captures BER for 2 transmit 2 receive MIMO V-BLAST ttansmission/reception for BPSK modulation in a flat fading independent Rayleigh channel, for the different equalizer structures discussed above.

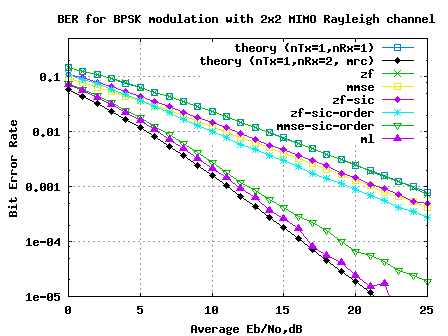
Figure: BER plot for 2 transmit 2 receive MIMO channel for BPSK modulation

Observations

1. The BER curve with ZF equalization for 2×2 MIMO channel is identical to BER plot for 1 transmit 1 receive system

2. Ordered variant of successive interference cancellation shows better performance than the simple successive interference cancellation

3. MMSE equalization with ordered successive interference cancellation provides performance which is slightly poorer than ML.

4. With ML equalization, we come close to the performance of 1 transmit 2 receive MRC case. We gain both throughput gain and diversity gain.

Reference

[DIG-COMM-BARRY-LEE-MESSERSCHMITT] Digital Communication: Third Edition, by John R. Barry, Edward A. Lee, David G. Messerschmitt

V-BLAST: An architeture for realizing very high data rates over the rich scattering wireless channel – P. W. Wolniansky, G. J. Foschini, G. D. Golden, R. A. Valenzuela.

67 thoughts on “Six equalizers for V-BLAST”

Areeb says:

January 30, 2013 at 9:55 pm

Hey Krishna ! 🙂

I am doing VBLAST detection… the program I am using is an OSIC detector function that implements VBLAST algorithm using MMSE (SINR based ordering), ZF (SNR based ordering) and column-norm based ordering. The function is as follows:

function [X_hat]=OSIC_detector(y,H,sigma2,NT,OSIC_type)
% Input
% y : Received signal, NRx1
% H : Channel matrix, NRxNT
% sigma2: Noise variance
% NT : Number of Tx antennas
% OSIC_type=1/2/3 for Post_detection_SINR/Column_max/Post_detection_SNR
% Output
% X_hat : Estimated signal, NTx1

if OSIC_type==1 % Post_detection_SINR
Order=[]; % Detection order
index_array=[1:NT]; % yet to be detected signal index

% V-BLAST
for stage=1:NT
Wmmse=inv(H’*H+sigma2*eye(NT+1-stage))*H’; % MMSE filter (Eq.(11.7))
WmmseH=Wmmse*H;
SINR=[];
for i=1:NT-(stage-1)
tmp= norm(WmmseH(i,[1:i-1 i+1:NT-(stage-1)]))^2+ sigma2*norm(Wmmse(i,:))^2;
SINR(i) = abs(Wmmse(i,i))^2/tmp; % SINR calculation Eq.(11.15)
end
[val_max,index_tmp] = max(SINR); % Ordering using SINR
Order = [Order index_array(index_tmp)];
index_array = index_array([1:index_tmp-1 index_tmp+1:end]);
x_tmp(stage) = Wmmse(index_tmp,:)*y; % MMSE filtering (Eq.(11.9))
X_hat(stage) = QPSK_slicer(x_tmp(stage)); % Slicing

y_tilde = y-H(:,index_tmp)*X_hat(stage); % Interference subtraction
H_tilde = H(:,[1:index_tmp-1 index_tmp+1:NT-(stage-1)]); % new H
H = H_tilde;
y = y_tilde;
end

X_hat(Order) = X_hat;

elseif OSIC_type==2 % Column_norm ordering detection
X_hat=zeros(NT,1);
G = inv(H); % Inverse of H
for i=1:NT % Column_norm calculation
norm_array(i) = norm(H(:,i));
end

[sorted_norm_array,Order_tmp] = sort(norm_array);
Order = wrev(Order_tmp);

% V-BLAST
for stage=1:NT
x_tmp = G(Order(stage),:)*y; % Tx signal estimation
X_hat(Order(stage)) = QPSK_slicer(x_tmp); % Slicing
y_tilde = y-H(:,Order(stage))*X_hat(Order(stage));
end

else % OSIC with Post_detection_SNR ordering
Order=[];
index_array=[1:NT]; % Set of indices of signals to be detected

% V-BLAST
for stage=1:NT
G = inv(H’*H)*H’;
norm_array=[];
for i=1:NT-(stage-1) % Detection ordering
norm_array(i) = norm(G(i,:));
end

[val_min,index_min] = min(norm_array); % Ordering in SNR
Order = [Order index_array(index_min)];
index_array = index_array([1:index_min-1 index_min+1:end]);
x_tmp(stage) = G(index_min,:)*y; % Tx signal estimation
X_hat(stage) = QPSK_slicer(x_tmp(stage)); % Slicing
y_tilde = y-H(:,index_min)*X_hat(stage); % Interference subtraction
H_tilde = H(:,[1:index_min-1 index_min+1:NT-(stage-1)]); % New H
H = H_tilde; y = y_tilde;
end

X_hat(Order) = X_hat;

end

Problem is its a function and I have to compare the BER of these three orderings using VBLAST… the code only gives the detected symbols X_hat..

I have used the program below, giving arguments of the function OSIC_detector(y,H,sigma2,NT,OSIC_type)

clc;clear all;close all;
M=2 ;
N=2 ;
EbN0 = 30;
OSIC_type=4;
NT=2;
total_bits = 1000;
j = 1;
H=(randn(N,M)+j*randn(N,M))/sqrt(2);
for EbN0=0:5:30
for i = 1:total_bits/2
N0 = 0.1.^(EbN0/10);
sigma2=(0.5/(10^(EbN0/10)));
x = randint(1,2,[0 3])’;
x_qam = qammod(x,4);
v=(randn(N,1)+j*randn(N,1))* sqrt(N0/2);
y=H*x+v;
xHat = OSIC_detector(y,H,sigma2,NT,OSIC_type);
xHat_det = qamdemod(xHat,4);
xbin = dec2bin(x,2);
xHat_det_bin = dec2bin(xHat_det,2);
z = bitxor(uint8(xbin),uint8(xHat_det_bin));
error_ite(i) = sum(sum(z));
end
snr(j) = EbN0;
bit_err(j) = sum(error_ite)./total_bits;
j = j+1;
end
semilogy(snr,bit_err);

The QPSK_slicer i am using is:

function [x_sliced] = QPSK_slicer(x,n)
sq05=1/sqrt(2); jsq05=j*sq05; n=length(x)
for i=1:length(x)
if imag(x(i))>real(x(i))
if imag(x(i))>-real(x(i)), x_sliced(i)=jsq05;
else x_sliced(i)=-sq05;
end
else
if imag(x(i))>-real(x(i)), x_sliced(i)=sq05;
else x_sliced(i)=-jsq05;
end
end
end

As such i haven’t found any problems in the logic of the above program but the results are extremely incorrect!… the BER I am getting is different every time!
most probably the error comes from the OSIC_function program. But i am not able to figure them out 🙁

PROBLEM: I am not getting any expected BER! results are too weird!

Please check them and let me know the possible errors in my program.

Reply
1. Krishna Sankar says:
  
  February 1, 2013 at 5:47 am
  
  @Areeb: Sorry, I wont be able to help with the coding. Please ensure that you have zero error rate in the case where noise is zero.
  
  Reply
Dar says:

January 2, 2013 at 12:34 am

Hi Krishna.
In articles about V-BLAST, it is always noted that “the number of receive antennas Nr must be at least as large as the number of transmit antennas Nt”.
Do you know that is why?

Reply
1. Krishna Sankar says:
  
  January 2, 2013 at 5:34 am
  
  @Dar: Well, one can think of the V-BLAST story as trying to solve for N unknowns, and to solve for N unknowns we need atleast N equations. The number of receive antennas form the N equations part. Helps?
  
  Reply
  1. Dar says:
    
    January 13, 2013 at 3:38 pm
    
    So you are saying, since we are implementing linear decoding like ZF and MMSE; we need N equations for N unknowns. So if we implement decoding using ML rather than ZF and MMSE; do we still have this constraint? What do you think?
    
    Reply
    1. Krishna Sankar says:
      
      January 17, 2013 at 5:30 am
      
      @Dar: Yes, the constraint holds good.
      
      Reply
  2. Dar says:
    
    January 16, 2013 at 1:10 pm
    
    So you are saying since we are using linear decoding algorithms we need N linearly independent equations for solving N unknowns. So if we rather use ML decoding algorithm does it mean we will not have such a constraint. What dou you think?
    
    Reply
    1. Krishna Sankar says:
      
      January 17, 2013 at 6:29 am
      
      @Dar: I think the constraint holds good.
      
      Reply
phani says:

November 23, 2012 at 2:51 pm

Sir
Please provide me the matlab code for Analysis and design of OFDM-IDMA systems
please help me it’s urgent
my mail id is phani08473@gmail.com

Reply
1. Krishna Sankar says:
  
  November 27, 2012 at 5:47 am
  
  @phani: sorry, do not know about ofdm-idma
  
  Reply
Samin says:

October 12, 2012 at 10:19 am

Hello sir
If it is possible, please send me the Matlab code of the above simulation.
Thank you very much
My email address: samin6182@gmail.com

Reply
1. Krishna Sankar says:
  
  October 17, 2012 at 6:16 am
  
  @Samin: The individual posts referred in this article has the simulation code
  
  Reply
Pingback: Symbol Error Rate (SER) for QPSK (4-QAM) modulation
Mary says:

August 21, 2012 at 8:45 pm

Hello Sir,

can I use this ‘V-BLAST’ simulation code to model a 2×2 MIMO system using spatial multiplexing and investigate the effect of the signal processing at the transmitter on the SNR at the receiver?

Many Thanks

Reply
1. Krishna Sankar says:
  
  August 22, 2012 at 8:25 am
  
  @Mary: Yes, please do so.
  
  Reply
ghahraman says:

July 9, 2012 at 10:45 am

hi , exiuseme i want matlab code Six equalizers for V-BLAST
BER for BPSK modulation with 2×2 MIMO Rayleigh channel
pleaze send me way email
my email is ghahraman26@yahoo.com

Reply
1. Krishna Sankar says:
  
  July 10, 2012 at 6:12 am
  
  @ghahraman: please refer to the individual posts in https://dsplog.com/tag/mimo
  
  Reply
ghahraman says:

July 5, 2012 at 6:31 pm

hi i want matlab code. pleaz send way e-mail for me. very tanks
my email is ghahraman26@yahoo.com

Reply
1. Krishna Sankar says:
  
  July 6, 2012 at 5:45 am
  
  @ghahraman: emailed you the instructions
  
  Reply
Pattaraporn says:

August 6, 2010 at 11:50 pm

hello sir,
I am student, I am working on 2X2 MIMO . I need a source about spatial Multiplexinf and space time coding for QAM Modulation or instructions for programming from you.

Thank you

Reply
1. Krishna Sankar says:
  
  August 10, 2010 at 5:05 am
  
  @Pattaraporn:
  Hope the links
  https://dsplog.com/tag/mimo/
  https://dsplog.com/tag/alamouti/
  helps.
  
  Reply
raj says:

November 25, 2009 at 10:34 am

Sir i will send you some references regarding to that, please send me your e-mail address.

Is there any different between MMSE detection and MMSE equalization, if yes than what is that?

thanks

Reply
1. Krishna Sankar says:
  
  December 7, 2009 at 4:31 am
  
  @raj: Well, am not sure. It depends on the problem which you are modeling. The MMSE algorithm can be used to ‘detect the arrival of the packet’ which is quite different from equalizing the packet which is corrupted by noise and interference.
  
  Reply
aydar says:

October 27, 2009 at 3:17 pm

wow, i didnt know that Reinaldo Valenzuela is one of the authors..

Reply
1. Krishna Sankar says:
  
  November 8, 2009 at 7:37 am
  
  @aydar: 🙂
  
  Reply
raj says:

October 26, 2009 at 4:06 pm

hi sir,
i want check the impact of MIMO (MMSE-OSIC) system on the higher-level protocol, wether it will be better idea for research?

And is there any other technique for MMSE detector, rathar than the mathamatical equation (H^H*H + I/snr)^-1*H^H), where can i find it?

Reply
1. Krishna Sankar says:
  
  November 7, 2009 at 7:10 am
  
  @raj:
  1/ What is higher level protocol?
  2/ In general the equation for MMSE is as the one listed above. You may find the derivation in typical text books.
  
  Reply
  1. raj says:
    
    November 12, 2009 at 10:51 am
    
    sir i want to check the of impact of MIMO (MMSE-OSIC) system on the transport control protocol (TCP) protocol.
    and is there any different between MMSE detection and MMSE equalization, if yes than what is that?
    
    Reply
    1. Krishna Sankar says:
      
      November 13, 2009 at 5:39 am
      
      @raj: MMSE-OSIC on TCP protocol, eh? How do you apply MMSE in the TCP framework. Can you please point me to some references.
      
      Reply
      1. raj says:
        
        November 18, 2009 at 12:52 pm
        
        Sir i will send you some references regarding to that, please send me your e-mail address.
        
        thanks
      2. Krishna Sankar says:
        
        December 6, 2009 at 3:51 pm
        
        @raj: Thanks. You can find my email listed in https://dsplog.com/contact-us/
      3. raj says:
        
        November 18, 2009 at 12:54 pm
        
        Is there any different between MMSE detection and MMSE equalization, if yes than what is that?
      4. Krishna Sankar says:
        
        December 6, 2009 at 3:52 pm
        
        @raj: Well, am not sure. It depends on the problem which you are modeling. The MMSE algorithm can be used to ‘detect the arrival of the packet’ which is quite different from equalizing the packet which is corrupted by noise and interference.
      5. raj says:
        
        December 16, 2009 at 10:30 pm
        
        hi sir,
        thanks for reply,
        but sir equalization and detection , both are same process and they are different from estimation, am i right?
        
        Is there any difference between SVD (singular value decomposition), SQRD (sorted QR decomposition), and decorrelating process?, b’cos ultimately they all belongs to set diagonal components of any matrix.
        
        What is the different between Sphere decoding (SD) and Lattice reduction?
        
        i am curious to wait for your replay,
        once again thanks for your great support.
      6. Krishna Sankar says:
        
        December 23, 2009 at 5:27 am
        
        @raj: my replies
        a/ both equalization and detection can be different
        b/ i think both svd and sqrd are different. have not studied much on this topic
        c/ have not studied in detail sphere decoding and lattice reduction. hence unable to comment
Egerue Nnamdi says:

October 8, 2009 at 2:58 pm

Hi all
Pls i am currently an MSC student in the UK and working on (OFDM) as my Dissertation. I am to investigate how to use Matlab to simulate the following channel impairment
1 Multipath Delay
2 Peak power Clipping
3 Channel Noise
4 Frequency selective fading
5 Intersymbol interference.
I am surpose to compare the performance of (OFDM) and BPSK, QPSK etc using the above channel impairments. currently the Matlab codes i have does not plot any thing. Pls i will appreciate if someone can help me out.

NNAMDI

Reply
1. Krishna Sankar says:
  
  October 12, 2009 at 5:27 am
  
  @Egerue: Hope the posts under https://dsplog.com/tag/ofdm address some of your queries. Good luck.
  
  Reply
William says:

October 6, 2009 at 12:29 pm

Hello Krishna,

My simulations show a little different results. In my results, the 2×2 BPSK ZF BER lacks the 1×1 BPSK BER by 3 dB. I believe this to be a sane result, because I have scaled the transmission power by 1/sqrt(2) to keep the total transmission power emitted by all antennas constant for a fare comparison between different schemes. Have you done this in your simulations? Similarly, my 2×2 ML BPSK transmission lacks the MRC by 5 dBs.

Reply
1. Krishna Sankar says:
  
  October 8, 2009 at 5:34 am
  
  @William: If you look @ the simulation in post https://dsplog.com/2008/10/24/mimo-zero-forcing/, it can be seen that I have scaled the transmit voltage (not power) by 1/sqrt(2). Scaling the transmit voltage by 1/sqrt(2) ensures that power on each arm is 1/2 and totals to unity.
  
  Further, from the Section 3.3 of book Fundamentals of Wireless Communication, David Tse, Pramod Viswanath, its mentioned that “BER for 2×2 MIMO channel in Rayleigh fading with Zero Forcing equalization is same as the BER derived for a 1×1 channel in Rayleigh fading.”
  
  Hope this helps.
  
  Reply
2. raj says:
  
  October 8, 2009 at 11:15 am
  
  Thank you sir,
  I have get the result for SIC using optimal ordering, but if I use V-BLAST with coding than the coding is perform before demultiplexing of data so data bits(symbols) get spreded spatially in channel and we have to decode them jointly at receiver which is not happened in H-BLAST (coding is done after demultiplexing) so for V-BLAST,
  
  1. How can the bits are decoded at the receiver? Should it require some change in programme?
  
  2. How many complexity operations are required in ML(maximum likelyhood), ZF, MMSE, ZF-SIC, MMSE-SIC, ZF-OSIC, MMSE-OSIC?
  
  sir very very thanks for showing interest in my queries, bye.
  
  Reply
  1. Krishna Sankar says:
    
    October 12, 2009 at 5:20 am
    
    @raj:
    1/ In V-BLAST, there is interference between parallel transmissions. At the receiver, we try to null the interference and recover the required data symbol.
    2/ I have not done precise calculations on the complexity difference between these algorithms.
    
    Reply
raj says:

September 19, 2009 at 11:54 am

hi sir,
I extremely thanks you to share this tremendous work in field of MIMO spatial multiplexing,
I am working in the same field , so i request you to share some details if you don’t mind
I have certain query about the V-BLAST programme,

1.traditionally BLAST scheme uses three different types of coding, V-BLAST, D-BLAST, H-BLAST, so this programme uses coding?

2. and one most important question is that What is the most recent possible research scope in this MIMO spatial multiplexing field?

Ones again thanks for showing interest in this field.

Reply
1. Krishna Sankar says:
  
  September 22, 2009 at 5:43 am
  
  @raj: My replies:
  1/ I used V-Blast where all transmit antennas transmit simultaneously.
  2/ One topic which interests me is to simplify the equalizer structure and reach ML like performance (Sphere decoding etc)
  
  Reply
  1. raj says:
    
    September 23, 2009 at 11:07 am
    
    Thank you for reply, but my question is that
    
    In V-BLAST , is there any kind of coding (e.g. convolution) is used? b’cos in programs ,I am not found any kind of coding at transmitter, if I want to use coding at transmitter than what changes require at receiver? particularly in case of V-BLAST & D-BLAST.
    
    In the programme of ZF-SIC with optimal ordering , you have assign channel with higher SNR to second stream (force-fully), but if I want to do SIC on the basis of original SNR values of symbol than would I get desired result?
    
    thx
    
    Reply
    1. Krishna Sankar says:
      
      October 1, 2009 at 5:15 am
      
      @raj: My replies
      1/ No, I have not assumed presence of coding in transmitter. However, even if coding is present, it will just be that the output of the equalizer will go to the decoder and the decoder will generate the raw bits.
      2/ I believe you meant optimal ordered successive interference cancellation. To do that select the stream having higher SNR. I have provided a post on Zero Forcing with optimal ordered successive interference cancellation.
      https://dsplog.com/2008/11/29/mimo-zf-sic-optimal-order/
      
      Hope this helps.
      
      Reply
Pingback: Bit Error Rate (BER) for BPSK modulation
Habib says:

July 10, 2009 at 5:44 pm

Hi there,
I am M.Sc researcher in IIUM. I am working on 2X2 MIMO channel sounder. I need an urgent help for a simulink model of MIMO transmitter. can you help me, how to call M-file in simulink. I have created an M-function or code generator. I need to ad this as a source of transmitter in simulink.

Thank you

Reply
1. Krishna Pillai says:
  
  July 15, 2009 at 4:59 am
  
  @Habib: Sorry, I have not worked with Simulink.
  
  Reply
  1. Ashok says:
    
    July 24, 2009 at 10:46 am
    
    Hi Habib,
    What kind of MIMO you need?
    STBC MIMO demo is there in simulink if you have communication tool box. Check the WiMax Model.
    For using matlab code use ‘Embedded MATLAB block’ in simulink.
    
    Reply
sohbet says:

July 2, 2009 at 6:11 pm

hi good thank you blog

Reply
Mark says:

June 6, 2009 at 12:10 pm

can you please give me the source code for the simulation. Thanks.

Reply
1. Krishna Pillai says:
  
  June 7, 2009 at 2:37 pm
  
  @Mark: The source code for each equalizer structure is provided as part of the individual articles. You may click the hyper link to see the articles in detail and obtain the source code.
  
  Reply
Alvina says:

May 7, 2009 at 4:55 pm

@benjamin u can find contact of krishna at

https://dsplog.com/contact-us/

Reply
benjamin.frank says:

May 6, 2009 at 8:14 am

Krishna Pillai,
I am right now calculating the ber versus snr in qpsk-ofdm environement,but the curve is not what we expected, it is different from the theory,maybe the code has some problems, how can i contact you?my mail address:benjamin.frank@163.com

Reply
1. Krishna Pillai says:
  
  May 12, 2009 at 5:12 am
  
  @benjamin.frank: Well, due to time constraints, I prefer not to debug the code. May I point you to a post on Symbol Error Rate with QPSK modulation in AWGN.
  https://dsplog.com/2007/11/06/symbol-error-rate-for-4-qam/
  
  Good luck.
  
  Reply
Alvina says:

April 29, 2009 at 2:20 pm

@krishna
can you please give me the source code for the simulation. Thanks.

Reply
1. Krishna Pillai says:
  
  April 30, 2009 at 5:43 am
  
  @Alvina: Matlab code for the curve for each receiver structure is present in the individual articles (links are present in the post). I just made a top level simulation to generate all the curves in one go.
  
  Reply
VC says:

April 27, 2009 at 10:48 pm

Hi, can you please send me the source codes for the simulations. Thanks a lot.

Reply
1. Krishna Pillai says:
  
  April 30, 2009 at 5:30 am
  
  @VC:Matlab code for the curve for each receiver structure is present in the individual articles (links are present in the post). I just made a top level simulation to generate all the curves in one go.
  
  Reply
ilhami gozcu says:

April 23, 2009 at 8:03 pm

Hi,

Thanks for the useful post. Is it posible to add the Matlab code of the simulation?

Reply
1. Krishna Pillai says:
  
  April 30, 2009 at 5:10 am
  
  @ilhami gozcu: Matlab code for the curve for each receiver structure is present in the individual articles (links are present in the post). I just made a top level simulation to generate all the curves in one go.
  
  Reply
saeed says:

April 22, 2009 at 8:26 am

thank you so much for this file .and i hope to give me some code about quality of service and call admission control because i’am research in this topic.
thanks

Reply
1. Krishna Pillai says:
  
  April 30, 2009 at 5:09 am
  
  @saeed: I have not tried modeling higher layer protocols like QoS, admission control etc. Good luck in your research.
  
  Reply
D1EG0 says:

April 21, 2009 at 9:38 pm

Can you put the matlab code of this graph for know how can I generate all the matrix.

Thanks

Reply
1. Krishna Pillai says:
  
  April 30, 2009 at 5:04 am
  
  @D1EG0: Matlab code for the curve for each receiver structure is present in the individual articles (links are present in the post). I just made a top level simulation to generate all the curves in one go.
  
  Reply
  1. benjamin.frank says:
    
    May 6, 2009 at 8:05 am
    
    after evaluating the bit error rate, can you consider the bit loading in ofdm scheme and in the receiver using V-blast or D-blast? thanks
    
    Reply
    1. Krishna Pillai says:
      
      May 12, 2009 at 5:10 am
      
      @benjamin.frank: I will surely post on MIMO OFDM using V-BLAST. D-BLAST is bit more sophisticated and I need to stuby more.
      
      Reply