In this post lets discuss a closed-loop transmit diversity scheme, where the transmitter has the knowledge of the channel. As there is a feedback path required from the receiver, to communicate the channel seen by the receiver to the transmitter, the scheme is called closed-loop transmit diversity scheme. Recall that the transmit diversity using Space Time Coding (Alamouti STBC) does not require the knowledge of the channel. In this post, we will restrict our discussion to a 2 transmit, 1 receive case. We will assume that the channel is a flat fading Rayleigh multipath channel and the modulation is BPSK.
Channel Model
1. We have 1 receive antennas and two transmit antenna.
2. The channel is flat fading – In simple terms, it means that the multipath channel has only one tap. So, the convolution operation reduces to a simple multiplication. For a more rigorous discussion on flat fading and frequency selective fading, may I urge you to review Chapter 15.3 Signal Time-Spreading from [DIGITAL COMMUNICATIONS: SKLAR]
3. The channel experienced by each receive antenna is randomly varying in time. For the receive antenna, each transmitted symbol gets multiplied by a randomly varying complex number
. As the channel under consideration is a Rayleigh channel, the real and imaginary parts of
are Gaussian distributed having mean
and variance
.
4. The channel experience by each transmit antenna to receive antenna is independent from the channel experienced by other transmit antennas.
5. On each receive antenna, the noise has the Gaussian probability density function with
with
and
.
6. At each transmit antenna, the channel is known.
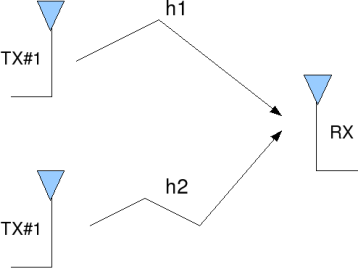
Figure: 2 transmit 1 receive beam steering
Transmit Beamforming
On the receive antenna, the received signal is,
where,
is the received symbol,
is the channel on the
transmit antenna,
is the transmitted symbol and
is the noise on the receive antenna.
When transmit beamforming is applied, we multiply the symbol from each transmit antenna with a complex number corresponding to the inverse of the phase of the channel so as to ensure that the signals add constructively at the receiver. In this scenario, the received signal is,
,
where,
and
.
In this case, the signal at the receiver is,
.
For equalization, we need to divide the received symbol with the new effective channel, i.e,
.
BER Simulation Model
The Matlab/Octave script performs the following
(a) Generate random binary sequence of +1’s and -1’s.
(b) Multiply the symbols with the beam steering matrics – corresponding to the phase of the channel
(c) Perform equalization at the receiver
(d) Perform hard decision decoding and count the bit errors
(e) Repeat for multiple values of and plot the simulation and theoretical results.
Click here to download Matlab/Octave script for simulting BER for BPSK in flat fading Rayleigh channel with and without beamforming
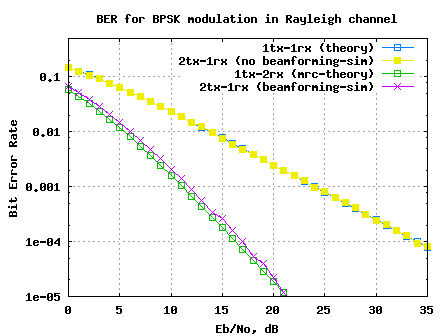
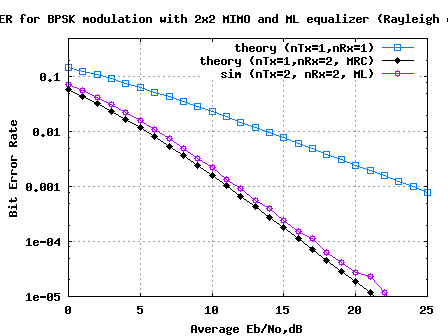
Figure: BER plot for 2 transmit 1 receive beamforming for BPSK in Rayleigh channel
Observations
1. Sending the same information on multiple transmit antenna does not provide diversity gain. Intuituvely, this is due to the fact that the effective channel in a 2 transmit antenna case is again a Rayleigh channel; hence the BER performance is identical to 1 transmit 1 receive Rayleigh channel case.
2. If the transmit symbols are multiplied by a complex phase to ensure that the phases align at the receiver, there is diversity gain. However, the BER performance seems to be slighly poorer than the 1 transmit 2 receive MRC case. I guess, the noise is scaled by in the case of transmit beamforming, whereas the noise scaling is different in the case of Maximal Ratio Combining. I need to study bit more for a precise answer.
Reference
[DIG-COMM-BARRY-LEE-MESSERSCHMITT] Digital Communication: Third Edition, by John R. Barry, Edward A. Lee, David G. Messerschmitt
hello,
can you equally send me the script of the beamforming to my email (ahmedamate@yahoo.com). interested in seeing the flow.
thank you
@Ahmed: The link to the simulation model is provided in the post.
hi Krishna
i wanna simulated 2*2 channel matrix, i use this code:
h=(randn(2,2)+1i*randn(2,2))/sqrt(4)
correct? or i should use sqrt(2)?
@ahmad: i reckon 1/sqrt(2) suffice.
Hi Krishna,
I am trying to do Transmit Beamforming for a 2×2 case (2 transmit and 2 receive).
So how will the received signal be?? Will it be something like this
[y1 ;y2]=[h11 h12;21 h22]*[s1;s2]+noise ??
@Tarun: The system model remains the same. If we do SVD beamforming, typically premultiply the transmit signal to ensure that the two streams does not interfere with each other …
thanks a lot mate
i want your help. I want to select a dissertation” Implementing adaptive array processing in MATLAB” means simulation in matlab. it easy or difficult do u have any model in matlab about it
thanks
@azhar: sorry, i do not have a model for that
I’m wondering in practice how to cancel the phasor at the transmitter simultaneously even if we know the channel phase terms to all the receiver antennas. Obviously at any time instant, you’ve got only one data at the transmitter but you want to cancel each phasor out at each receiving link.
@linkin8834: we can multiply the same data with different phasors, dont we?
In “y1 = sum(h.*sr,1) + 10^(-Eb_N0_dB(ii)/20)*n; ” why use ” 10^(-Eb_N0_dB(ii)/20)*n; ” not “10^(-Eb_N0_dB(ii)/10)*n; ” ?
@flz: the noise term n is a voltage term.
Hello,
I just want to ask why the informed 2×1 coincides with the 1×2 system regarding the BER? As we know we have ‘Array Gain’ in the latter scenario and we don’t have it in the former one.
Does this have to do with Eb/No instead of SNR?
Thanks
Osama
@Osama: We have an array in the transmitter and at the transmitter we know the channel, dont we? We can use that information to get the performance gains
Hi krishna,
this is raja, i am doing research in the area of transmit beamforming by using SVD and i have use the rayleigh channel and MRC at the receiver…here mainly i concentrate on using different modulatin BPSK and 16-QAM and got the graph for BER vs SNR……i dont know how to derive the equations for BER calculation…..can u help me please…….i am waiting for ur reply plz…….
@Raja: Where you able to get the simulation models up?
will you please email me the matlab codes to simulate the average throughput for a multibeam system compared with a single beam system
@seynabou diene: Sorry, did not understand multi-beam vs single-beam. Is it multi-user vs single-user?
Hi Raja
Can you email me the modified transmit beamforming code.
My email is shakeelj2k at yahoo dot com
Hi Raja
will you please email me the script which you discussed in your post for beamforming my email sr2923 at gmail.com
grateful to you
Can anyone help me in knowing what is meant by transmit and receive chain in Matlab and what are the blocks involved in this ?
@Paresh: Well… transmit chain is the transmitter which sends out information which is unknown to the transmitter. The receiver chain tries to extract these bits based on what it observed. 🙂
Hi, I love your blog very much, and i have learned a lot from it.
One question, for the beamforming, i was wondering when we need to multiply the steering vector?
is it the case of beamforming at both transmitter and reciever?
Thanks.
@victor: Typically, we multiply the beamsteering coefficients at the transmitter.
Thanks for your reply.
The beamsteering coefficients in this case is w = exp(conj(h)), am i right?
Does it mean that when multiplying this coeffcient, we can cancel the effect due to Rayleigh Channel and extract the signal out directly without using any equilizer?
Regards,
@victor: My replies
1) Yes
2) The multiplication ensures that there will be no phase reversals. However, you might want to use equalizers to take care of amplitude variations especially when QAM modulation is employed.
i think the outage probability and BER will be equivalent of transmit beamforming and receive beamforming, when path loss and number of antennas are same at tranmit antennas in tranmit beamforing and receive antennas at receive beamforming. so final equations should be the same theoriticaly like MRC!
@lee waen: By receive beamforming, I think you meant Maximal Ratio Combining, correct?
Mathematically, there is a subtle difference between the transmit beamforming and receive MRC, though the end result is close. (as seen in the figure, BER with beamforming is very near to the performance obtained by MRC case).
Can you please point me to a reference for the statements which you have made.
yes, receving beamforming meant MRC.
Actually i think MRC and transmit beamforming are equal in mathematically with the reference of this book, which is iam going to mail you on ur id, this have a proof too.
@lee waen: Thanks for the email.
May I point out a subtle difference between the beamforming mentioned in this paper,
compared to the discussion in this post.
In this paper, the pre-coding matrix at the transmitter is the conjugate of the channel i.e w = h^H.
In this post, I have assumed that the pre-coding matrix is the phase of the conjugate of the channel. i.e w = exp(conj(h))
Quite likely this is the reason for the difference in performance. Hope you agree. Please share your thoughts.
Hi, I think somehow only half the noise power gets added to the BPSK symbols in your code. If you do QPSK instead of BPSK the code would now hold good , since for both QPSK and BPSK the BER is the same. but in this code for BPSK , i guess the adding of noise is incorrect. what are your thoughts on this ?
@karanth: I think your statement is incorrect. Recall that for BPSK, the noise only on the real arm affects the reception. Hope the post on BER for BPSK in AWGN helps. https://dsplog.com/2007/08/05/bit-error-probability-for-bpsk-modulation/
Hi thanks for the reply. I am suspecting the code for this reason: say we dont scale by sqrt(Nt) for each transmit chain, then the system is equivalent to the MRC case and the BER should be same as in MRC. I find that without power scaling in this code, the 2×1 MRT performs better than 1×2 …which cant be possible please check it.
@karanth: The scaling by 1/sqrt(nTx) is to make the total power radiated from all the transmit antennas to one. If we do not do that, then its not a fair comparison with MRC case. Agree?
Additional comments:
“say we dont scale by sqrt(Nt) for each transmit chain, then the system is equivalent to the MRC case and the BER should be same as in MRC.”
[krishna] Incorrect. With the MRC case, the SNR on each receive chain is |h_i|^2Eb/N0. With beamforming case, the SNR is (|h1|+|h2|)^2*1/2*Eb/N0. Both are not mathematically equivalent.
Agree?
If you work out the resulting average SNR gain (post processing gain) for both MRT and MRC, they are the same if there is no power/amplitude scaling. Therby the BERs should be same.
This should be quite intuitive since we have equal power transmitted or received in both cases for same number of antennas either at Tx end or Rx end.
However, in your case, if you limit transmit power for MRT then the gains differ.
@karanth: To have a fair comparison, shouldn’t we have similar average transmit power in both the cases?
Hi krishna,
I am doing project based on paper “A New Beamforming Structure Based on Transmit-MRC for Closed-Loop MIMO Systems” by Seok-Hwan Park, Heunchul Lee, Sang-Rim Lee, and Inkyu Lee, Senior Member, IEEE,Can you please send me reference matlab code for svd beamforming.
@Lakshmana: Sorry, I have not yet posted articles on SVD based beamforming. Hope to do so in the near future.
Hey! Your blog is very nice.
Visit my blog now..
I forward ur blog to all of my friendss…
My blog is about my creativity .
My hobbies are writing quotations of types Success,..
Include all my hobbies in my blog..
Visit now and enjoy my creativity . please leave a comment .
If u enter my blog you can see the web design sample,free downlaod,online money,..
How can activate ads in my blog? Please tell.
Hi, Krishna
For 2×1 with no beamforming. What algorith did you use to feed the input in e.g. Alamouti, or Spatial multipexing or else?
@Marcus: I just send the same information on both the antenna, and that gives the same results as sending on only one antenna.
Also, could you upload the modified script too, or is this script the modified one?
@UP: The script is the latest one.
Hi. Could you please refer to to some basic tutorial on transmit beamforming ?
@UP: I was hoping that this post is indeed a basic introduction to transmit beamforming, aint it? 😉
hi Krishna
can u tell me the formula to find weighting or beamforming vektor.
please send me the modified script.my email add is riris_novie@yahoo.com
thx a lot.
@susanti: Given that we know the channel at the transmitter, the weighting factor just computes the conjugate of the phase of the channel. For eg, if the channel is [h1, h2] the weighting factor used at the transmitter is [conj(angle(h1) angle(h2)].
The script present in the code is the latest one. There is only minor modifications for clarity. Good luck.
thank khrisna,.
if the weighting factor just compute the conjugate of the phase of the channel, how about other method to get weighting factor such a LMS,RLS,Eigen-beam?
would you explain the difference use?
@susanti: Well, amo not familiar with the schemes which you were proposing. Can you please provide me a reference.
Hi Krishna,
Tx beamforming should be better than MRC. The manner you apply the beamforming vector is not right. If you give me your email address I can mail you the modified script.
regards,
Raja
can u plz send me the modified script as well.
my email add is alvina_23@yahoo.co.uk
thnx a lot.
@Alvina: As you may have seen from the discussion with Mr. Raja, there is no modification required in the script. The plots and the script are correct. However, as Raja has suggested, for clarity, I have defined a variable called hEff in the script.
Could you please send the modified script to me as well. I need to work on this area too.
My email is mazdaspring@hotmail.com
@Paul: As you may have seen from the discussion with Mr. Raja, there is no modification required in the script. The plots and the script are correct. However, as Raja has suggested, for clarity, I have defined a variable called hEff in the script.
@Raja: Can you please explain the correct way of applying beamforming. To benefit other readers of this post, may I request you to reply to this comment itself. In anycase, you wish to contact me over email, please find my details in https://dsplog.com/contact-us/
Hi Krishna,
I will send you the modified script to your email. The script might be a bit slow.
The major things to look for ar the following:
1. y = h*w*s = heff*s
—> w is the beam forming vector
—> s are symbols to be transmitted
—> heff is the effective channel
after beamforming
2. During Equalization
s = y./heff
Regards,
Raja
hi Raja
can u plz send me the script as well.my email add is alvina_23@yahoo.co.uk
thhx a lot.
@Raja: Thanks for mailing the code. I looked at the code and ran the simulations. My observation is that, you are seeing a better performance for 2×1 beamforming case – because the scaling of transmit power by 1/sqrt(nTx) is not performed for the beamforming case.
Further, scaling by 1/sqrt(nTx) is required, as we are sending the same information multiplied by the phase on both the antennas.
I mailed you the script with minor updations for your review. Please share your feedback.
Thanks again.
Hi Krishna,
You are right regarding the scaling and the result. I would also like to point out that heff is a 1×1 matrix not a 1×2 matrix.It does not change the result but i wanted to point it to you for correctness.
I guess beamforming with 1 rx-antenna provides the same performance with MRC-rx diversity if not poorer. A good comparison would be to compare between beamforming and alamouti(both with or without rx diversity).
Regards,
Raja
@Raja: Thanks for confirming the result. For notational clarity, I just modified the script to define the variable hEff. However, as we agree, the results still remain the same.
Yes, 2tx-1rx beamforming seems to be almost comparable (slightly poorer) than 1tx-2rx MRC.
As we had seen from the results with 2transmit-1receive Alamouti STBC, https://dsplog.com/2008/10/16/alamouti-stbc/, the Alamouti STBC performance is around 3dB poorer than the 1transmit-2receive MRC. So the 2transmit-1receive beamforming is better than the 2transmit-1receive alamouti by around 2.7dB. Agree?
Hi Krishna,
You are right regarding the performance between beamforming(with Channel Knowledge) and Alamouti.
Best Regards,
Raja
Hello Krishna,
First off let me thank you for posting relevant topics on signal processing for wireless comm, I visit this website quite often and I find the info useful.
I believe MRC outperforms Tx beamforming because there is a 3 dB penalty for Tx beamforming. For 2×1 transmit beamforming the signal energy is halved at the transmitter in order to constrain the output Tx power to be the same as in the MRC case for comparison.
Regards,
Senay
@Senay: Well, in this simulations, I do not think its the 3dB penality in transmit power which is coming into play. However, am unable to pinpoint the cause too.